Harilik lineaarne regressioonmudel

Vähimruutude meetodi rakendamisel leitakse lisaks parameetrite punkthinnangutele ka mudeli standardvea ja parameetrite standardvigade hinnangud. Nende põhjal saab leida parameetrite usalduspiirid ja mis veel olulisem, saab leida testimiseks vajalikud t-statistikud.

Vähimruutude meetodi kasutamisel minimeeritakse jääkide ruutude summat \(\sum\limits_{i = 1}^n {u_i^2} \) ja tulemuseks on mingi arv. Selle jagamisel vabadusastmete arvuga n-k , kus n on valimi maht ja k mudeli parameetrite arv, saadakse  mudeli dispersiooni hinnang

\({s^2} = \frac{{\sum\limits_{i = 1}^n {u_i^2} }}{{n - k}} = \frac{{\sum\limits_{i = 1}^n {{{\left( {{y_i} - \hat a{x_i} - \hat b} \right)}^2}} }}{{n - k}}\)

Ruutjuur sellest on mudeli standardviga (standard error of regression)

\(se = \sqrt {{s^2}} \)

Parameetrite standardvead leitakse mudeli standardvea põhjal

\(se(\hat b) = se\sqrt {\frac{1}{n} + \frac{{{{\bar x}^2}}}{{\sum {{{\left( {{x_i} - \bar x} \right)}^2}} }}} \)

\(se(\hat a) = \frac{{se}}{{\sqrt {\sum {{{\left( {{x_i} - \bar x} \right)}^2}} } }}\)

Näitena vaatame elektrienergia tarbimise mudeli täielikku aruannet programmis Gretl.

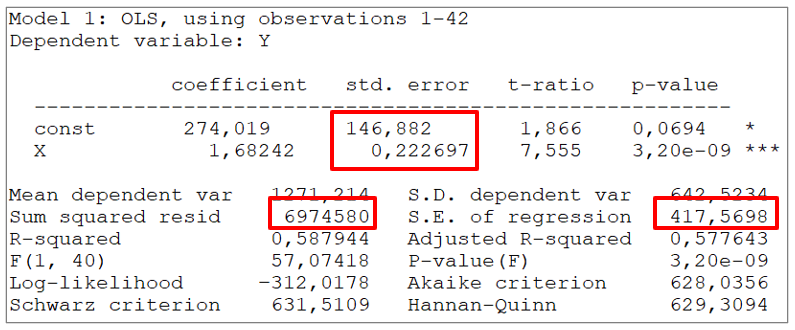
Jääkliikmete ruutude summa (Sum squared resid) on 6974580. Valimi maht on 42 ja mudeli parameetrite arv 2. Mudeli standardviga (S.E. of regression) on siis

\(se = \sqrt {\frac{{\sum\limits_{i = 1}^n {u_i^2} }}{{n - 2}}}  = \sqrt {\frac{{6974580}}{{42 - 2}}}  \approx 417,5698\)

Kui nüüd leida  \(\bar x ^2= 351310\) ja \(\sum {\left( x_i - \bar x \right)^2} =3515822\), mis aruandes pole kuvatud, siis parameetrite standardvead

\(se(b) = se\sqrt {\frac{1}{n} + \frac{{{{\bar x}^2}}}{{\sum {{{\left( {{x_i} - \bar x} \right)}^2}} }}} =417,6598 \sqrt{\frac {1}{42} + \frac{ 351310}{3515822}} =146,882\)

\(se(a) = \frac{{se}}{{\sqrt {\sum {{{\left( {{x_i} - \bar x} \right)}^2}} } }} = \frac{{417,5698}}{{\sqrt {3515822} }} = 0,222697\)

Parameetrite standardvead on aruande tabeli veerus std. error ja loomulikult ei pea me neid ise arvutama. Aga peame aru saama nende arvutusvalemitest, sest see võimaldab vaatlusi paremini organiseerida. Kui vaatame veelkord parameetri a standardvea valemit, siis  nimetajas on  \(\sum {\left( x_i - \bar x \right)^2} \), mis isleoomustab tunnuse x väärtuste hajumist ümber aritmeetilise keskmise. Kui see hajumine on väike, st nimetaja on väike, siis murd on suur. Järelikult, kui x väärtused hajuvad vähe, tuleb parameetri standardviga suur. Sama kehtib ka parameetri b standardvea kohta.

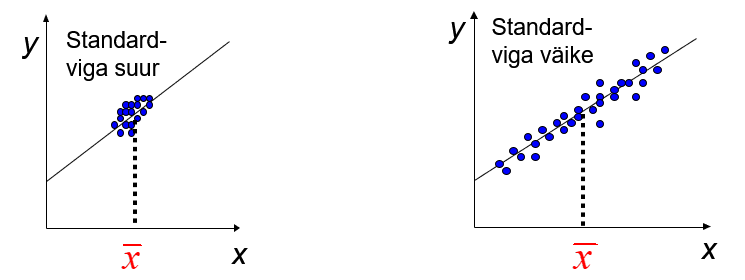
Täpsemate hinnangute saamiseks peavad tunnuse x väärtused võimalikult palju hajuma.  Seda peab silmas pidama valimi moodustamisel. 

Parameetrite hinnangute usalduspiiride leidmisel lähtutakse sellest, et  hinnangute standardiseeritud erinevused tegelikest väärtustest alluvad t jaotusele vabadusastmete arvuga \(\nu  = n - k\), kus n on valimi maht ja k parameetrite arv mudelis (hariliku lineaarse mudeli korral k=2):

\(\frac{{\hat a - a}}{{se(\hat a)}} \sim t(\nu )\quad ,\quad \frac{{\hat b - b}}{{se(\hat b)}} \sim t(\nu )\)

\(\hat a \pm t_{\alpha /2}\,(\nu ) se(\hat a) \;\;\; \hat b \pm t_{\alpha /2}\,(\nu ) se(\hat b)\)

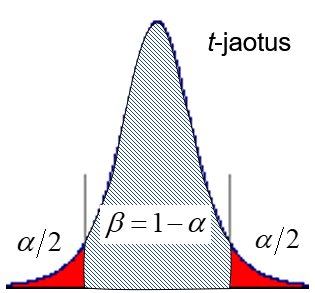
Viirutatud ala on tõenäosus, et parameetri tegelik väärtus jääb usalduspiiridesse. Punane ala: tõenäosus, et tegelik väärtus on väljaspool usalduspiire.

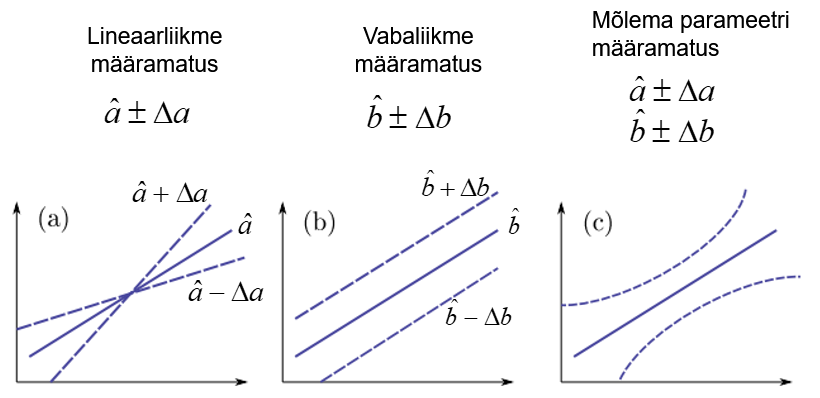
See, et mudeli parameetrite hinnangud ei vasta täpselt tegelikele väärtustele, vaid tegelikud väärtused jäävad usaldatavusega β usalduspiiridesse, tähendab, et valimi põhjal leitud regressioonsirge ei vasta täpselt tegelikule sirgele. Tegelik sirge jääb teatud veakoridori. Joonisel on tootud eraldi kummagi parameetri määramatusest ning mõlema parameetri määramatusest tingitud sirge asendi määramatus.

Tabelarvusprogrammis Excel kuvatakse parameetrite usalduspiirid regressioonmudeli hindamise aruande viimastes veergudes. Ökonomeetria pakettide aruannetes parameetrite usalduspiire tavaliselt ei kuvata, kuid neid saab eraldi vaadata. Programmis Gretl näiteks preale mudeli hindamist Analysis->Confidence intervals for coefficients. Järgnevalt on esitatud Houthakkeri elektrienergia tarbimise mudeli parameetrite usalduspiirid usaldatavusega 95%.

Siit näeme, et kui aastane sissetulek x suureneb ühiku ehk 1 GBP võrra, siis elektrienergia tarbimise suurenemine jääb tõenäosusega 95% vahemikku 1,23 kuni 2,13 kWh aastas. Näeme ka seda, et kui sissetulek puudub (x=0), siis tarbimine võib olla 0 kWh, sest 0 jääb konstandi usaldusvahemiku sisse.