Harilik lineaarne regressioonmudel
11. Lineariseeritavad mudelid
Peatükis 9, kus vaadeldi erindi mõju, oli toodud näide 209 ettevõtte käibe jaotusest. See oli väga asümmeetriline, valimis esinesid üksikud ettevõtted, mille käive oli ülejäänud ettevõtetega võrreldes väga suur. Asümmeetria vähendamiseks käivet logaritmiti.
Vaatleme nüüd samade ettevõtete andmete põhjal koostatud regressioonmudelit, kus ettevõtte tegevjuhi palk (salary) sõltub ettevõtte käibest (sales). Palk on tuhandetes dollarites ja käive miljonites dollarites.
Kui kasutame lineaarset mudelit, siis mudeli hindamine annab
\(\widehat {{\rm{salary}}} = 0,015{\rm{sales}} +1174 \quad \quad \quad {R^2} = 0,015\) (1)
Mudeli kirjeldusvõime on väga madal. Hajumisdiagrammi analüüsimine näitab, et esinevad erindid. Diagrammilt on näha, et lisaks mõnele väga suure käibega ettevõttele on ka mõned sellised, kus käive on väike, aga tegevjuhi palk väga suur.
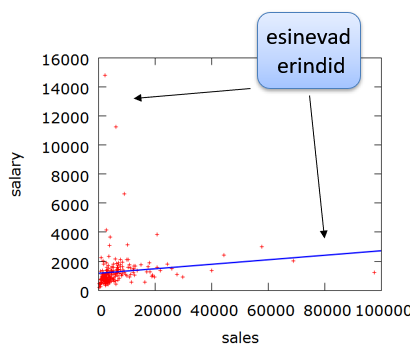
Logaritmime mõlemat tunnust. Mudelit, kus mõlemad tunnused on logaritmitud, nimetatakse log-log mudeliks. Tulemuseks on
\( \ln \widehat {{\rm{salary}}} = 0,257 \ln {\rm{sales}} +4,8 \quad \quad \quad {R^2} = 0,211\) (2)
Mudeli kirjeldusvõime tõusis. Hajumisdiagrammil erindeid enam ei esine.
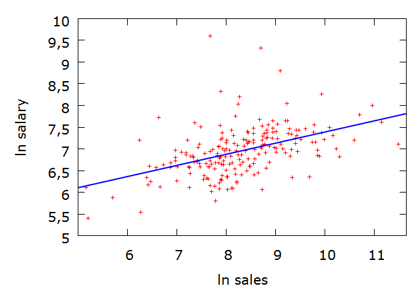
Järelikult log-log mudel kirjeldab seda seost oluliselt paremini.
Tuletame meelde, et lineaarse mudeli kordaja näitab, kui palju muutub y, kui x muutub 1 võrra. Seega lineaarne mudel (1) ütleb, et kui ettevõtte käive on 1 mln $ võrra suurem, siis ettevõtte juhi töötasu on 0,015 tuh $ võrra suurem.
Mida näitab aga log-log mudeli kordaja?
Log-log mudeli kordaja näitab, mitu % muutub Y, kui X suureneb 1%. Seega log-log mudeli kordaja on elastsuskordaja.
Toodud näites mudelist (2): kui ettevõtte käive on 1% suurem, siis ettevõtte juhi töötasu on 0,257% suurem.
Lineaarse mudeli ja log-log mudeli erinevus:
- lineaarne mudel: piirkalduvus (sirge tõus) on konstantne;
- log-log mudel: elastsuskordaja on konstantne.
Tuletame ühtlasi meelde, mis on elastsuskordaja. Elastsuskordaja E seob omavahel tunnuste x ja y suhtelisi muutusi:
\(\frac{\Delta y} {y} = E \frac {\Delta x}{x}\)
Kui avaldame sellest seosest E, siis
\(E = \frac {x}{y} \frac{\Delta y}{\Delta x}\)
Kui me tahame leida elastsuskordaja väärtust ühes punktis (punktelastsus), tuleb lõplikud muudud Δy ja Δx asendada lõpmatult väikeste muutudega ehk diferentsiaalidega dy ja dx:
\(E = \frac {x}{y}\frac{{dy}}{{dx}}\) (3)
kus \(\frac{{dy}}{{dx}}\) on y tuletis x järgi.
Kirjutame välja log-log mudeli üldkuju
\( \ln y= E \ln x +c +u \) (4)
Siit tuleb ka vajadus kasutada log-log mudelis naturaallogaritme. Kui rakendame elastsuskordaja arvutamise valemit (3) seosele (4), siis saame, et ln x ees olev kordaja on elastsuskordaja. Kui kasutaksime näiteks kümnendlogaritme, oleks elastsuskordaja leidmine mudeli parameetrite põhjal oluliselt keerulisem.
Tunnuste x ja y suhtes on mudel (4) mittelineaarne. Aga logaritmitud tunnuste suhtes on mudel lineaarne. Seda on lihtne näha, kui võtame kasutusele uued tähistused \(w=\ln y\) ja \(z= \ln x\). Siis saab log-log mudeli (4) kirja panna kujul
\(w= E z +c +u \)
ning on näha, et tunnuste w ja z suhtes on mudel lineaarne. Järelikult parameerite E ja c leidmiseks saab kasutada harilikku vähimruutude meetodit.
Vaatame ka üht teist mittelineaarset mudelit. Analüüsime USA SKP muutumist aastatel 1800 kuni 2009. SKP on miljardites dollarites.
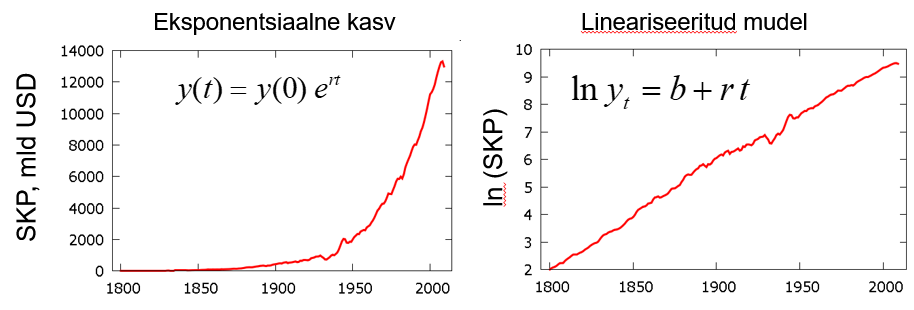
Vasakpoolsel diagrammil on esitatud SKP muutus ajas. Graafikult on näha, et tegemist on eksponentsiaalse kasvuga, mida kirjeldab mudel
\( y(t)=y(0) e^{rt}\), (5)
kus t on aeg aastates, t=1 aastal 1800. Põhimõtteliselt võib ajamuutuja defineerida ka nii, et vaadeldava perioodi alguses t=0, kuid ökonomeetriapakettides võetakse ajamuutuja esimeseks väärtuseks alati 1. Parameeter r on kasvumäär ja see näitab, mitu protsenti keskmiselt on SKP igal aastal kasvanud. See mudel on mittelineaarne ja kasvumäära r leidmiseks ei saa kasutada harilikku vähimruutude meetodit. Kui aga mudelit lineariseerida, saame aja t suhtes lineaarse mudeli. Parempoolsel diagrammil on näha, et suurus \(\ln y\) muutub ajas ligikaudu lineaarselt. Selle mudeli parameetreid on võimalik hinnata hariliku vähimruutude meetodi OLS abil. Sõltuva tunnuse logaritmimine teisendab eksponentsiaalse kõvera lineaarseks.
Toome ära eksponentsiaalse mudeli (5) lineariseerimise etapid, st millised matemaatilised teisendused tuleb teha.
\(y(t) = y(0){e^{rt}}\)
Logaritmime võrduse mõlemaid pooli
\(\ln y(t) = \ln \left( {y(0){e^{rt}}} \right)\)
Kasutame logaritmi omadust: korrutise logaritm on tegurite logaritmide summa
\(\ln y(t) = \ln y(0) + \ln {e^{rt}}\)
Teise liidetava juures arvestame seda, et \(\ln e ^{rt} = rt\). Sest naturaallogaritm näitab ju seda, millisele astmele tuleb arv e võtta, et saada logaritmi all olev avaldis, milleks antud juhul on \(e^{rt}\). Loomulikult astmele \(rt\).
\(\ln y(t) = \ln y(0) + rt\)
Võtame nüüd vabaliikme tähistamiseks kasutusele tähe b
\(b = \ln y(0)\) (6)
Saimegi aja t suhtes lineaarse mudeli
\(\ln y(t) = b + rt\) (7)
Sellist mudelit, kus sõltuv tunnus y on logaritmitud, aga seletav tunnus on mudelis lineaarselt, nimetatakse log-lin mudeliks.
Kasutades nüüd andmeid USA SKP kohta, hindame mudelit \(\ln {SKP_t} = r\,t + b + {u_t}\), kus SKP on miljardites dollarites ja t aeg aastates (t=1 aastal 1800). Mudeli hindamise aruanne on järgmine:
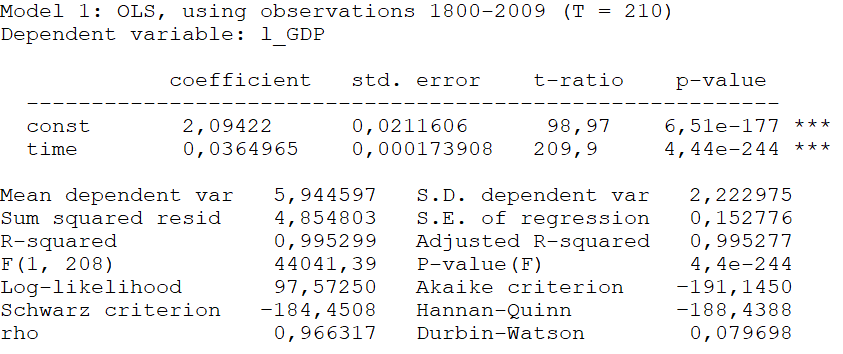
Näeme, et ajamuutuja time ees oleva kordaja (kasvumäära) olulisuse tõenäosus on 4,44·10-244 < 0,05, st kasvumäär on statistiliselt oluline. Paneme kirja saadud mudeli kujul (7)
\(\begin{array}{rccl}\ln {\widehat {SKP}_t} & = &2,094 + &0,03650t\quad \quad {R^2} = 0,995 \quad \quad T = 210\\& \;&(0,021)& (0,00017)\end{array}\)
USA SKP kasvumäär r on olnud keskmiselt 3,65% aastas.
Järgmisel diagrammil on logaritmitud SKP tegelikud väärtused (punane joon) ja mudelväärtused (sinine).
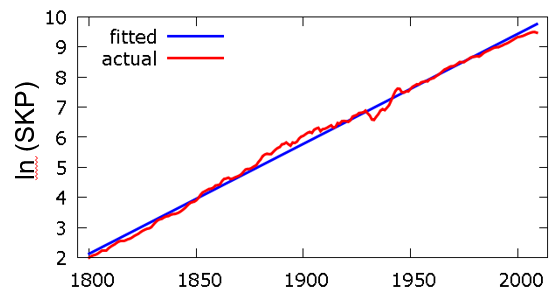
Teades kasvumäära r, võime kirja panna ka SKP kasvu mudeli eksponentsiaalsel kujul (5). Selleks tuleb aga enne arvutada eksponentsiaalses mudelis olev konstant y(0). Selle saame leida, kui arvestame eksponentsiaalse mudeli lineariseerimisel kasutusele võetud tähistust lineaarse mudeli vabaliikme kohta (6). Kuna b väärtus on regressioonanalüüsi abil hinnatud, b= 2,094, siis
\(y(0)= e^{2,094} \approx 8,12\)
Nüüd SKP kasvu mudel eksponentsiaalsel kujul
\(\widehat{SKP}=8,12 e^{0,0365t}\),
kus SKP on miljardites dollarites ja t aastates, t=1 aastal 1800.
Seda mudelit võime kasutada ka prognoosimiseks, eeldades, et keskmine kasvumäär on konstantne. Leiame mudeli järgi SKP väärtuse aastal 2019. Siis t=220. Paneme selle mudelisse ja arvutame välja:
\(\widehat{SKP}(220)=8,12 e^{0,0365\cdot 220}\approx 24,9\cdot 10^3\)
Järelikult mudel annab 2019. aasta USA SKP prognoositavaks väärtuseks 24,9 triljonit dollarit. Tegelik väärtus oli 21,433 triljonit dollarit (The World Bank)
Sageli sobib mudelina kasutada ruutfunktsiooni
\(y=ax^2+bx+c\)
Ka seda saame lineariseerida, kui võtame kasutusele uue tähistuse \(z=x^2\). Saame lineaarse mudeli, kus on kaks tunnust z ja x:
\(y=az+bx+c\)
Mitmese regressioonmudeli hindamine on analoogne hariliku lineaarse mudeli hindamisega. Kasutatakse harilikku vähimruutude meetodit OLS. Lähemalt vaatame seda järgmises teemas.
Niimoodi, kasutades tunnuste teisendamist, saab lineariseerida erinevaid mittelineaarseid mudeleid. Lineariseerimine on vajalik selleks, et mudeli parameetrite hindamiseks saaksime kasutada OLS meetodit.
Toome ära tähtsamad ökonomeetrias kasutatavad mudelid. Esimene mudel on lineaarne, ülejäänud mittelineaarsed, kuid lineariseeritavad. Tabelis on toodud ka valemid piirkalduvuse ja elastsuskordaja arvutamiseks.
| Mudeli nimetus | Mudeli kuju | Piirkalduvus \(\frac{d y}{d x}\) |
Elastsuskordaja \(\frac{x}{y}\frac{d y}{d x}\) |
|---|---|---|---|
| lineaarne mudel | \(y=b+ax+u\) | a | \(a\frac{x}{y}\) |
| log-log mudel | \(\ln y =b+a \ln x +u\) | \(a\frac{y}{x}\) | a |
| log-lin mudel | \(\ln y =b +ax+u\) | ay | ax |
| lin-log mudel | \(y = b + a \ln x +u\) | \(a\frac{1}{x}\) | \(a\frac{1}{y}\) |
| ruutfunktsioon | \(y=ax^2 + bx +c +u\) | \(2ax+b\) | \(\frac{x}{y}(2ax + b)\) |
| hüperboolne mudel | \(y = b + a \frac{1}{x} +u\) | \(-a\frac{1}{x^2}\) | \(-a\frac{1}{xy}\) |
On näha, et palju tuleb tegemist teha logaritmidega, seepärast on kasulik üle korrata logaritmide arvutamise ja teisendamisega seotud põhitõed. Selleks võib kasutada antud teema juures eraldi toodud materjali "Logaritmide kordamiseks".