Hüpoteeside testimine

Site:	TalTech Moodle
Course:	MEM5250 Ökonomeetria
Book:	Hüpoteeside testimine

Printed by:	Guest user
Date:	Sunday, 29 September 2024, 5:24 AM

Description

Kirjandus: A. Sauga "Statistika õpik majanduseriala üliõpilastele" peatükk 7.

1. Hüpoteeside testimise vajadus
2. Hüpoteeside testimise põhialused

1. Hüpoteeside testimise vajadus

Lisaks regressioonmudeli parameetrite hindamisele on vaja statistiliselt testida ka mitmeid hüpoteese. Hüpoteeside testimine peale mudeli hindamist on vajalik selleks, et olla kindel: mudel on usaldusväärne ja selle põhjal võib teha järeldusi. Järgnevalt vaatame kolme peamist põhjust hüpoteeside testimiseks.

1. Regressioonmudeli juhuslikkus

Oletame, et meil on valim mahuga n=10 ja soovime hinnata mudelit, mis kirjeldab tunnuse y sõltuvust tunnusest x.

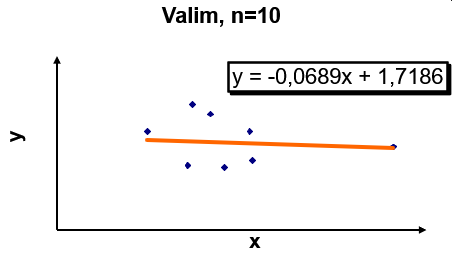
Valimi põhjal hinnatud mudel näitab, et x ja y vahel on negatiivne seos.

Aga tegelikult ei pruugi tunnus y sõltuda tunnusest x. Kogumis on näha, et y erinevus väärtusest 1,775 on juhuslik ja ei sõltu tunnuse x väärtustest.

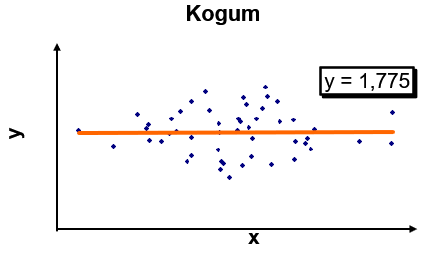
See tähendab, et tegelik regressioonmudel on \(y=1,775+u\), kus u on juhuslik komponent ja y juhuslikult kõigub ümber oma keskväärtuse 1,775.

Ökonomeetrilise mudeli abil

Püütakse tõestada, et Y on seotud suurustega X₁, X₂, ....
Kui seos on, siis kas positiivne või negatiivne.
Parameetrite arvväärtused on tihti vähem olulised.

Järelikult on meil vaja tõestada, et valimi põhjal hinnatud mudeli parameetrid on oluliselt erinevad nullist.

2. Kas parameetrite hinnangud on nihketa?

Hindame mudelit \(y = {\beta _0} + {\beta _1}{x_1} + {\beta _2}{x_2} + u\), st leiame parameetrite β₀, β₁ ja β₂hinnangud, kasutades harilikku vähimruutude meetodit OLS. Kas leitud hinnangud on nihketa? Ainult siis, kui on täidetud hariliku vähimruutude meetodi kasutamise eeldused.

Nende eelduste kehtimist tuleb kontrollida! Selleks on mitmesugused testid, mida vaatame järgmiste teemade juures.

3. Erinevate mudelite võrdlemine

Tihti tuleb võrrelda erinevaid mudeleid ja otsustada, kumb mudel on parem. Näiteks olgu meil

Mudel 1: y= β₀+ β₁ x₁ +u

Mudel 2: y= β₀+ β₁ x₁ + β₂ x₂ +u

Kas mudelid on oluliselt erinevad, st kas tunnuse x₂ sissetoomine on põhjendatud?

Teine näide

Mudel 1: y= β₀+ β₁ x₁ +u

Mudel 2: y= β₀+ β₁ x₁ + β₂ x₁² +u

Kas mudelid on oluliselt erinevad, st kas sõltuvus on lineaarne või mittelineaarne?

2. Hüpoteeside testimise põhialused

Põhjalikult on hüpoteeside testimine esitatud õpiku A.Sauga "Statistika õpik majanduseriala üliõpilastele" peatükis 7. Siin esitatakse lühidalt vaid kõige olulisem, et korrata varem õpitut. Kes pole aga varem statistikat õppinud, tuleks lugeda õpikut ja külastada A.Sauga Statistika kursust Moodles. Vt Statistika kordamine.

2.1. Nullhüpotees, sisukas hüpotees ja teststatistik

Hüpoteeside statistilisel testimisel tuleb alati formuleerida hüpoteeside paar: nullhüpotees ja sisukas hüpotees. Sõltuvalt testimise tulemusest võetakse siis vastu kas nullhüpotees või sisukas hüpotees.

Nullhüpotees H₀: miski võrdub millegagi (erinevus on null). Näiteks

kogumi keskväärtus μ=μ₀
kogumi A keskväärtus võrdub kogumi B keskväärtusega, μ_A=μ_B
mudeli mingi parameeter on null, seos puudub: β_i=0

Sisukas ehk alternatiivne hüpotees H₁: võrdus ei kehti.

Hüpoteesipaar võib olla püstitatud kas kahepoolselt (erinevuse suund pole oluline) või ühepoolselt. Näiteks kogumi keskväärtuse testimisel

	Kahepoolne hüpotees	Ühepoolne hüpotees, vasak	Ühepoolne hüpotees, parem
Nullhüpotees H₀	μ = μ₀	μ ≥μ₀	μ ≤ μ₀
Sisukas hüpotees H₁	μ ≠ μ₀	μ < μ₀	μ >μ₀

Otsustamiseks kasutatakse juhuvalimit. Me teame, et juhuvalimi põhjal saadud hinnang on juhuslik suurus ja kindlasti erineb nullhüpoteesiga püstitatud võrdusest. Aga kui suur see erinevus võib olla, et võime öelda: nullhüpotees on ümber lükatud ja tuleb vastu võtta sisukas hüpotees? Vaja kriteeriumi!

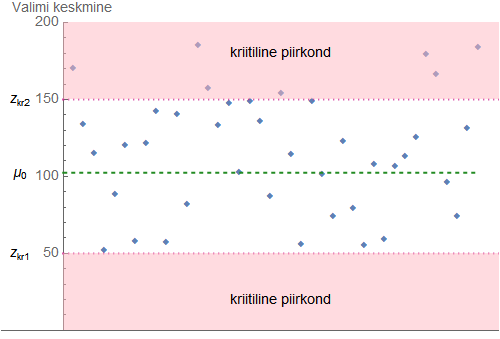
Järgmises interaktiivses demos on kahest erinevast üldkogumist võetud juhuvalimid. Ühe kogumi korral nullhüpotees kehtib, teise kogumi korral ei kehti. Kuidas ühe juhuvalimi põhjal otsustada, kas see tuleb kogumist, mille korral nullhüpotees kehtib, või tuleb see kogumist, mille korrral nullhüpotees ei kehti?

Demos oli tegemist kogumi keskväärtuse testimisega. Analoogselt toimub otsustamine igasuguse statistilise testimise korral.

Otsustamiseks vajaliku statistilise kriteeriumi leidmiseks kasutatakse sobivat teststatistikut.
Valimi andmete põhjal arvutatakse teststatistiku empiiriline väärtus.

Sõltuvalt sellest, mida testitakse, on konkreetsed arvutusvalemid erinevad.
z-test, t-test, F-test, χ2-test, ....

Teststatistiku empiirilist väärtust võrreldakse vastava kriitilise väärtusega ja võetakse vastu otsus.

Kui empiiriline väärtus on nullist kaugemal kui kriitiline (asub kriitilises piirkonnas), on nullhüpotees ümber lükatud ja võetakse vastu sisukas hüpotees.
Kui empiiriline väärtus on nullile lähemal kui kriitiline (ei ole kriitilises piirkonnas), võetakse vastu nullhüpotees.

Erinevate teststatistikute kriitiliste väärtuste leidmiseks olid vanasti statistilised tabelid. Näiteks tabelid õpikust Tamhane, A. C. " Statistical Analysis of Designed Experiments: Theory and application" Tänapäeval on võimalus kasutada arvutit. Näiteks Excelis on olemas funktsioonid erinevate teststatistikute kriitiliste väärtuste jaoks. Samuti on programmis Gretl Tools menüüs Statistical tables. Kui aga andmed on Gretli andmebaasis, siis kõik testimise jaoks vajalikud arvutused tehakse automaatselt, kui valime menüüst meid huvitava testi.

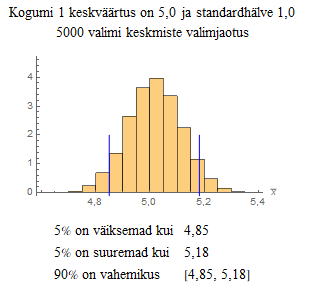
Mille alusel aga põhimõtteliselt leitakse kriitiline väärtus, millest alates on nullhüpotees ümber lükatud ja võetakse vastu sisukas hüpotees? Selle selgitamiseks on järgmine demo.

Demos vaadati, kuidas leitakse kriitilised väärtused kogumi keskväärtuse testimisel. Põhimõte on aga kõikide testide korral ühesugune: lähtutakse sellest, kuidas jaotuvad kehtiva nullhüpoteesi korral teststatistiku väärtused. Iga teststatistiku jaoks on vastav teoreetiline jaotusseadus, millele see statistik allub ja millest võetakse kriitilised väärtused.

Jaotusseadus seob omavahel tõenäosuse ja statistiku väärtused. Pideva juhusliku suuruse korral tõenäosus, et see suurus omab mingit kindlat väärtust, on 0. Nullist erinev on tõenäosus, et juhuslik suurus on väiksem mingist väärtusest või suurem mingist väärtusest või jääb mingisse vahemikku. Järgneval joonisel on statistiku z jaotusseadus, kus horisontaalteljel on z väärtused. Tõenäosust kirjeldab kõvera alla jääv pindala. Rohelise piirkonna pindala on tõenäosus, et z<a.

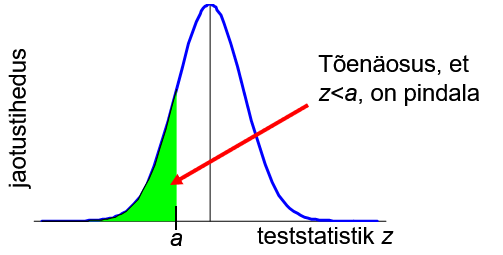
Jaotusseadust võib kasutada kahel moel.

Anda ette tõenäosus, et z on mingist väärtusest väiksem (suurem) ja leida vastav väärtus a.
Anda ette väärtus a ja leida tõenäosus, et z on sellest väiksem (või suurem).

Siit tuleb ka kaks võimalust otsustamaks, kumb hüpotees tuleb vastu võtta.

2.2. Teststatistiku empiirilise väärtuse võrdlemine kriitilisega

Esimene võimalus otsuse vastuvõtmiseks, kui valimi põhjal on teststatistiku empiiriline väärtus leitud. Anname ette lubatud tõenäosuse (olulisuse nivoo) ja jaotusseadusest leiame sellele vastava teststatistiku väärtuse. Nii näiteks tehti eelmises demos: anti ette olulisuse nivoo 0,1, 0,05 või 0,01 ja leiti sellele vastav teststatistik, mis on kriitiliseks väärtuseks. Seejärel saab valimi põhjal arvutatud teststatistikut võrrelda kriitilise väärtusega. Nullhüpotees lükatakse tagasi, kui valimi põhjal leitud empiiriline väärtus langeb kriitilisse piirkonda. Järgnevas demos näed, millistel tingimustel võetakse vastu nullhüpotees ja millal sisukas hüpotees.

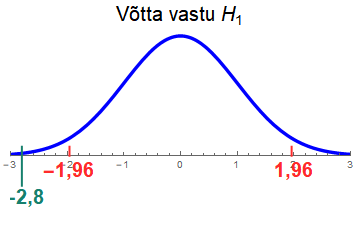
Seega olulisuse nivoole vastav teststatistiku väärtus on kriitiline väärtus. Kahepoolse hüpoteesi korral on vasakpoolne (negatiivne) ja parempoolne (positiivne) kriitiline väärtus ning kriitiline piirkond jaguneb kaheks. Ühepoolse hüpoteesi korral on üks kriitiline väärtus ning kriitiline piirkond jääb sellest ühele poole - nullist kaugemale. Nii kahepoolse kui ühepoolse hüpoteesi korral moodustavad kriitilise piirkonna need väärtused, mis on nullist kaugemal kui kriitiline väärtus.

Näiteks kriitilised väärtused kahepoolse z-testi korral, kui olulisuse nivooks on 0,05, on -1,96 ja 1,96. Alljärgneval joonisel on kriitiline piirkond viirutatud ja kui valimi põhjal arvutatud teststatistiku väärtus langeb sinna, tuleb nullhüpotees tagasi lükata ja vastu võtta sisukas hüpotees.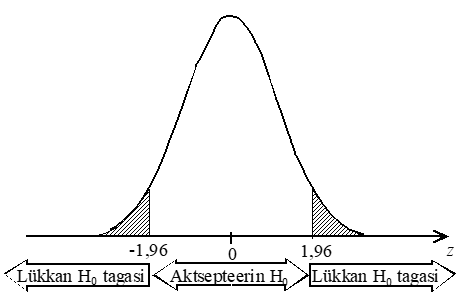

2.3. Olulisuse tõenäosuse võrdlemine olulisuse nivooga

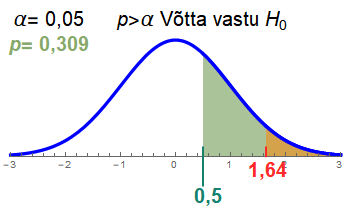
Teine võimalus otsustamiseks. Kui meil on teststatistiku empiiriline väärtus valimi põhjal leitud, saame jaotusseadusest leida sellele vastava tõenäosuse. Seda nimetatakse olulisuse tõenäosuseks ja tähistuseks on p (ingl p-value). Nüüd saame seda olulisuse tõenäosust võrrelda olulisuse nivooga α, mis on kriitilisele vastav tõenäosus. Nullhüpotees lükatakse tagasi, kui p<α.

Järgmises demos on demonstreeritud, kuidas kasutada otsuse vastuvõtmiseks olulisuse tõenäosust.

Olulisuse tõenäosus näitab sisuliselt, kui hästi valim sobib nullhüpoteesiga. Mida väiksem on olulisuse tõenäosus, seda väiksem on võimalus, et kehtib nullhüpotees.

Kaks meetodit: teststatistiku empiirilise väärtuse võrdlemine kriitilisega ja olulisuse tõenäosuse võrdlemine olulisuse nivooga, on ekvivalentsed, annavad sama tulemuse. Kasutatakse seda, mis konkreetses situatsioonis on mugavam. Ökonomeetriapaketid kuvavad testimise aruannetes teststatistikule vastava olulisuse tõenäosuse p ja siis on mugav kasutada just seda viimast võimalust.

Näiteks soovime teada, kas valim on tulnud kogumist, mille keskväärtus on suurem kui 5.

H₀ : μ≤ 5, H₁ : μ> 5

Valim on Gretli andmebaasis ja keskväärtuse testimise aruanne Gretlis:

Valimi maht on 609. Seejärel on leitud valimi keskmine ja standardhälve ning teststatistik t. Järgnevalt on t-jaotusest vabadusastmete arvuga 608 (st n-1) leitud väärtusele 51,7132 vastav olulisuse tõeäosus p kahepoolse hüpoteesi jaoks (two-tailed p-value) ja ühepoolse hüpoteesi jaoks (one-tailed). Kuna tegemist oli ühepoolse hüpoteesiga, vaatame viimast. Olulisuse nivooks võtame 0,05.

4,4·10^-225 < 0,05

Järelikult nullhüpotees on ümber lükatud ja võtame vastu sisuka hüpoteesi: see valim tuleb kogumist, mille keskväärtus on suurem kui 5.

Kõige sagedamini kasutatav olulisuse nivoo on 0,05. Kuid mõnikord kasutatakse ka nivood 0,1 või 0,01. Olulisuse nivoo valib uuringu läbiviija. Kui nivooks on 0,05, siis tõenäosus, et valimi põhjal lükkame tagasi kehtiva nullhüpoteesi, on väiksem kui 0,05. Seda nägime ühes eelnevas simulatsioonis, kus kehtiva nullhüpoteesi korral oli 5% selliseid valimeid, mille põhjal leitud teststatistik ületas kriitilise.

2.4. Kahte liiki vead

Hüpoteeside testimisel võib tegelikkusel olla kaks võimalust: nullhüpotees kehtib või nullhüpotees ei kehti. Kumb situatsioon on, seda me ei tea. Valimi põhjal tehtud otsuseid võib ka olla kaks: võtame nullhüpoteesi vastu või lükkame selle tagasi. Kokku saame 4 erinevat võimalust, mida illustreerib järgmine tabel.

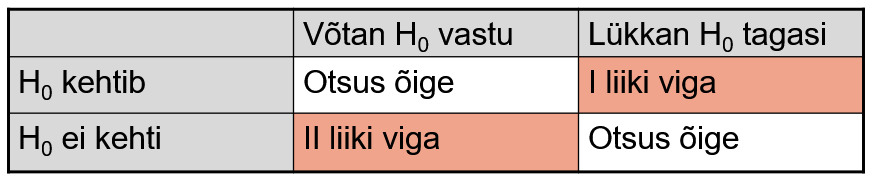
Seega on kahte liiki vigu. Kui me valimi põhjal lükkame nullhüpoteesi tagasi, võib otsus olla õige, aga võib esineda ka I liiki viga. Kui meile satub valim, mille põhjal võtame nullhüpoteesi vastu, võib samuti otsus olla õige, aga võib esineda ka II liiki viga. Olulisuse nivoo α on I liiki vea ülempiir. Kuidas olulisuse nivoo muutmine mõjutab I ja II liiki vea esinemise tõenäosust, näeb järgmises demos.

Seega olulisuse nivoo alandamine ehk α väärtuse vähendamine

vähendab I liiki vea tõenäosust;
suurendab II liiki vea tõenäosust.

I ja II liiki vea tagajärjed võivad olla erineva raskusega. Loomulik on vähendada selle vea tõenäosust, mille tagajärg on raskem. See sõltub konkreetsest situatsioonist, aga enamasti on raskema tagajärjega kehtiva nullhüpoteesi tagasilükkamine, st I liiki viga.

2.5. Kokkuvõte

Kokkuvõte hüpoteeside testimisest.

Püstitakse hüpoteesipaar: nullhüpotees ja sisukas hüpotees.
Valitakse sobiv teststatistik.
Valimi põhjal leitakse selle empiiriline väärtus.
Võetakse ette olulisuse nivoo (tavaliselt 0,05).
Võrreldakse

kas empiirilist ja kriitilist väärtust;
või olulisuse tõenäosust p ja olulisuse nivood α.

Otsustatakse, kumb hüpotees tuleb vastu võtta.

Kui empiiriline väärtus on nullist kaugemal kui kriitiline (ehk p < α), on nullhüpotees ümber lükatud ja tuleb vastu võtta sisukas hüpotees.