Harilik lineaarne regressioonmudel
| Site: | TalTech Moodle |
| Course: | MEM5250 Ökonomeetria |
| Book: | Harilik lineaarne regressioonmudel |
| Printed by: | Guest user |
| Date: | Sunday, 29 September 2024, 5:17 AM |
Description
Kirjandus: A. Sauga "Statistika õpik majanduseriala üliõpilastele" ptk 8.1-8.3, 9.1-9.7, 9.12, 9.16, 9.17.
Table of contents
- 1. Seos kahe tunnuse vahel: kovariatsioon ja korrelatsioon
- 2. Tinglik keskväärtus ja regressioonmudel
- 3. Harilik vähimruutude meetod.
- 4. Lineaarse mudeli tõlgendamine
- 5. Parameetrite standardvead
- 6. Parameetrite testimine
- 7. Determinatsioonikordaja
- 8. Mudeli korrektne esitamine
- 9. Erindi mõju
- 10. Vabaliikme olemasolu
- 11. Lineariseeritavad mudelid
1. Seos kahe tunnuse vahel: kovariatsioon ja korrelatsioon
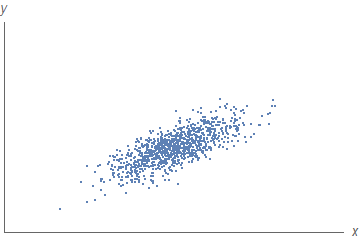
Olgu meil kaks arvulist tunnust x ja y ning n objekti, mille jaoks on nende tunnuste väärtused teada. Siis saame moodustada n punktipaari (xi, yi) ja kanda need punktid x-y teljestikku. Sellist diagrammi nimetatakse hajumisdiagrammiks (scatter diagram).
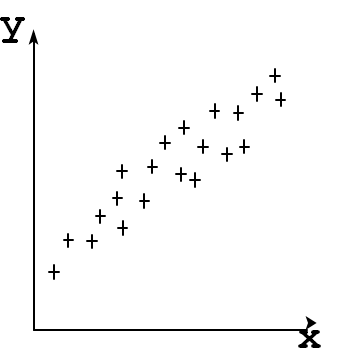
Hajumisdiagrammilt näeme, et kui x suureneb, siis keskmiselt suureneb ka y. Seega nende tunnuste vahel on seos. Ka järgmisel hajumisdiagrammil on tunnuste x ja y vahel seos, kuid punktid on rohkem hajunud.
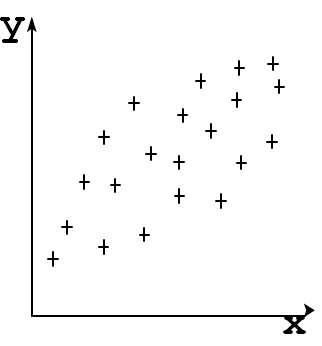
Kuidas väljendada selle seose tugevust kvantitatiivselt?
Ühe suuruse hajumist väljendab dispersioon
\({\sigma ^2} = E\left[ {{{\left( {X - {\mu _X}} \right)}^2}} \right]\),
kus E tähistab keskväärtust ja \({\mu _X} = E[X]\) on suuruse X keskväärtus. Diskreetseid väärtusi omava tunnuse korral \({\sigma ^2} = \frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {{x_i} - \bar x} \right)}^2}} \)
Kahe suuruse koosmuutumist väljendab kovariatsioon
\({\sigma _{XY}} = E\left[ {\left( {X - {\mu _X}} \right)\left( {Y - {\mu _Y}} \right)} \right]\)
Termin kovariatsioon tähendab koos muutumist (covariation). Diskreetseid väärtusi omava tunnuse korral
\({\sigma _{XY}} = \frac{1}{n}\sum\limits_{i = 1}^n {\left( {{x_i} - \bar x} \right)\left( {{y_i} - \bar y} \right)} \).
Erinevalt dispersioonist võib kovariatsioon olla nii positiivne kui ka negatiivne ja jääb vahemikku
\( - {\sigma _X}{\sigma _Y} < {\sigma _{XY}} < {\sigma _X}{\sigma _Y}\)
kus \(\sigma _X\) ja \(\sigma _Y\) on vastavalt tunnuste X ja Y standardhälbed.
Positiivne kovariatsioon: suurematele X väärtustele vastavad keskmiselt suuremad Y väärtused, väiksematele X väärtustele väiksemad Y väärtused.
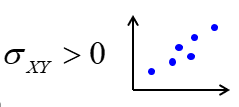
Negatiivne kovariatsioon: suurematele X väärtustele vastavad keskmiselt väiksemad Y väärtused, väiksematele X väärtustele suuremad Y väärtused.
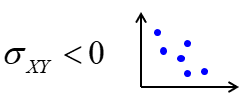
Kovariatsiooni omadused.
- Sümmeetrilisus \({\sigma _{XY}} = {\sigma _{YX}}\)
- Kui X=Y, siis \({\sigma _{XX}} = \sigma _X^2\)
-
Kovariatsioon on dispersiooni üldistus.
-
Dispersioon on kovariatsiooni erijuht: kovariatsioon iseendaga.
- Sõltumatute
juhuslike suuruste kovariatsioon on võrdne nulliga, \({\sigma _{XY}} = 0\)
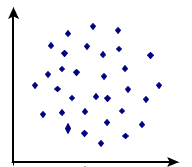
- Rõhutada tuleb, et vastupidine ei kehti, st kui kovariatsioon on null
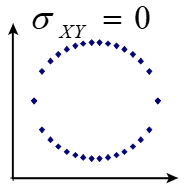 ,
ei pruugi suurused olla sõltumatud. Näiteks joonisel on tunnuste vahel tugev mittelineaarne seos, kuid kovariatsioon sellise punktiparve korral on 0.
,
ei pruugi suurused olla sõltumatud. Näiteks joonisel on tunnuste vahel tugev mittelineaarne seos, kuid kovariatsioon sellise punktiparve korral on 0. - Kui σXY ≠ 0, siis nimetatakse suurusi X ja Y korreleeruvateks.
Kovariatsiooni puudus on, et see on ühikuga suurus ja seetõttu pole võimalik võrrelda erinevates ühikutes antud tunnustepaaride kovariatsiooni. Valemist tulenevalt on kovariatsiooni ühikuks tunnuse X ühik korda tunnuse Y ühik. Näiteks tahame võrrelda, kumb suurus on Eesti maakondades tugevamini seotud töötuse määraga (%), kas keskmine kuupalk (€) või sündinud ettevõtete arv aastas. Leides vastavad kovariatsioonid, saame:
kovariatsioon töötuse määra ja keskmise kuupalga vahel -84,9 % ·€
kovariatsioon töötuse määra ja sündinud ettevõtete arvu vahel -480 % ·ettevõtet
Näeme, et mõlemad sosed on negatiivsed, st mõlema tunnuse tõustes töötuse määr väheneb, aga kummaga on töötuse määr tugevamini seotud? Leitud arve ei saa võrrelda, sest need on erinevates ühikutes. Ja me ei saa ka hinnata seda, kas seos on tugev või nõrk, sest me ei tea, milline kovariatsiooni väärtus vastab perfektsele seosele. Selle võib küll eraldi välja arvutada, see on standardhälvete korrutis.
Seepärast normeeritakse kovariatsiooni nii, et saaksime ühikuta suuruse ja selle absoluutväärtuse maksimaalne väärtus oleks 1. Võrratusest \( - {\sigma _X}{\sigma _Y} < {\sigma _{XY}} < {\sigma _X}{\sigma _Y}\) näeme, et selleks tuleb kovariatsioon läbi jagada standardhälvete korrutisega. Niimoodi leitud suurus on korrelatsioonikordaja
\({r_{XY}} = \frac{{{\sigma _{XY}}}}{{{\sigma _X}{\sigma _Y}}}=\frac{\sum(x_i - \bar x)(y_i - \bar y)}{n \sigma _x \sigma _y}\)
Korrelatsioonikordaja on ühikuta suurus ning selle väärtus on -1 ja 1 vahel:
\( - 1 < {r_{XY}} < 1\)
- Korrelatsioonikordaja absoluutväärtus näitab seose tugevust.
- Korrelatsioonikordaja märk näitab seose suunda: positiivne või negatiivne.
Näiteks olgu meil tunnused A, B ja C. Soovime teada saada, kumma tunnusega on A tugevamini seotud, kas tunnusega B või tunnusega C. Leiame vastavad korrelatsioonikordajad:
rAB= 0,58 ja rAC = -0,87.
Nagu näha, on A ja C vahel tugevam seos kui A ja B vahel, sest korrelatsioonikordaja absoluutväärtus on suurem.
Testi ennast, kas oskad korrelatsioonikordajate põhjal teha õigeid järeldusi.
Rõhutada tuleb veel seda, et korrelatsioonikordaja näitab lineaarse seose tugevust, kui hästi on punktid koondunud ümber sirge. Seepärast nimetatakse seda ka lineaarseks korrelatsioonikordajaks. Mittelineaarse seose tugevuse hindamiseks see näitaja ei sobi. Siis kasutatakse näiteks Spearmani astakkorrelatsiooni.
Järgmises demos saad uurida, kuidas on omavahel seotud lineaarne korrelatsioonikordaja ja punktiparv hajumisdiagrammil.
Edasi vaatame üht reaalsetel andmetel põhinevat näidet. H.S. Houthakker analüüsis oma artiklis "Some Calculations on Electricity Consumption in Great Britain." , millega on seotud elektrienergia tarbimine Suurbritannia erinevates linnades. Andmed pärinesid 42 linnast aastatest 1937-38. Tarbija sissetuleku ja elektrienergia tarbimise vahel oli positiivne korrelatsioon, r=0,767. Hinna ja tarbimise vahel oli nõrk negatiivne korrelatsioon, r = -0,274.
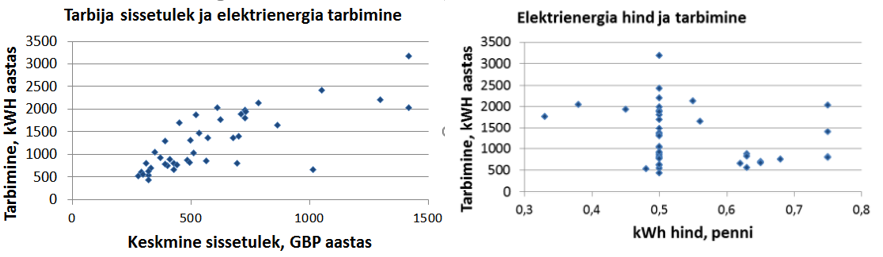
Nagu näha, on tarbija sissetuleku ja elektrienergia tarbimise vahel päris tugev seos. Edasi tekib küsimus: kas on võimalik leida seda seost kirjeldavat matemaatilist mudelit? Et teades tarbija sissetulekut, saaks prognoosida elektrienergia keskmist tarbimist. On küll võimalik ja selleks tuleb hinnata vastavat regressioonmudelit.
2. Tinglik keskväärtus ja regressioonmudel
Regressioonmudelini jõudmiseks tuleb kõigepalt tutvuda sellise suurusega nagu tinglik keskväärtus.
Eesti meeste keskmine pikkus on 179 cm. Selle võib kirja panna nii: E[PIKKUS] = 179 cm. See on tingimusteta keskväärtus (unconditional mean). On arusaadav, et Eesti meeste pikkused varieeruvad ümber selle keskväärtuse. Ühe konkreetse mehe korral PIKKUS= 179 + u , kus u on juhuslik komponent. Konkreetse mehe pikkus sõltub paljudest teguritest, mida see juhuslik tegur arvestab.
Poisslapse pikkus aga sõltub vanusest ning lisaks paljudest muudest teguritest. Näiteks 2-16 aastase poisslapse keskmine pikkus sentimeetrites
\({\rm{E}}\left[ {{\rm{PIKKUS}}\left| {{\rm{VANUS}}} \right.} \right] = 80,4 + 6 \cdot {\rm{VANUS}}\)
\({\rm{PIKKUS}} = 80,4 + 6 \cdot {\rm{VANUS}} + u\)
Seega, kui juhusliku suuruse Y keskväärtus sõltub juhusliku suuruse X väärtustest, on tegemist tingliku keskväärtusega, mida üldiselt tähistatakse
\({\rm{E}}\left[ {Y\left| X \right.} \right]\)
Konkreetse poisslapse pikkuse avaldises on kaks osa
- deterministlik komponent 80,4 + 6 · VANUS, mis on üheselt määratud vanusega
- juhuslik komponent u
Seda näidet üldistades: regressioonmudel koosneb deterministlikust ja juhuslikust komponendist:
y = deterministlik komponent + juhuslik komponent
Tinglik keskväärtus on deterministlik komponent ning regressioonmudeli üldkuju võime kirja panna ka nii\(y{\rm{ = E}}\left[ {Y\left| X \right.} \right] + u\)
Deterministlik komponent on mingi konkreetne matemaatiline funktsioon. Näiteks lineaarse regressioonmudeli y=ax+b+u korral ax+b on deterministlik komponent ehk tinglik keskväärtus ja u juhuslik komponent. Algul vaatlemegi lineaarset mudelit, mis on kõige lihtsam. Teema lõpus tutvume ka mõningate mittelineaarsete mudelitega.
Regressioonanalüüs uurib juhuslike suuruste vahelist sõltuvust ja võimalusi selle funktsionaalseks kirjeldamiseks etteantud valemi põhjal. See tähendab, et mudeli kuju (lineaarne, ruutfunktsioon , logaritmiline, ....) tuleb analüüsi teostajal ette anda. Regressioonanalüüsi käigus leitakse regressioonmudeli deterministlik komponent, st leitakse vastava matemaatilise funktsiooni parameetrite hinnangud. Juhuslikku komponenti leida ei saa, kuid me teame, et see eksisteerib ja seepärast tuleb see kindlasti regressioonmudelisse lisada. Kui me seda mudelisse kirja ei pane, siis näiteks poisslaste pikkuse korral tähendaks see, et kõik samas vanuses poisslapsed on sama pikkusega, mis on vale.
Kuidas siis leida regressioonmudelit, mis kirjeldab elektrienergia tarbimise sõltvuvust tarbija sissetulekust? Kasutame lineaarset mudelit y= ax+b+u , kus x on keskmine sissetulek (GBP asstas) ja y tarbimine (kWh aastas). Meil tuleb olemasoleva valimi põhjal leida mudeli parameetrite a ja b hinnangud, kasutades sobivat hindamismeetodit. Neid on mitmeid.
Olulisemad regressioonmudeli parameetrite hindamismeetodid.
- Vähimruutude meetod
- kõige tuntum
- minimeeritakse hälvete ruutude summat
- jaguneb
- harilik vähimruutude meetod OLS (Ordinary Least Squares) lineaarse mudeli korral;
- mittelineaarne vähimruutude meetod NLS (Nonlinear Least Squares);
- üldistatud vähimruutude meetod GLS (Generalized Least Squares).
- Suurima tõepära meetod MLE (Maximum Likelihood Estimation)
-
leitakse parameetrite hinnangud, mille korral antud valimi tõenäosus on kõige suurem;
-
kasutatakse peamiselt tõenäosusmudelite korral.
3. Harilik vähimruutude meetod.
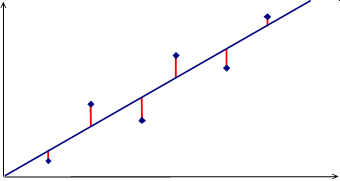
Olgu meil mingi valim n objektist, millel on kaks tunnust, st meil on arvupaarid (xi, yi), i=1,..., n. Diagrammil on need arvupaarid kujutatud punktidena.
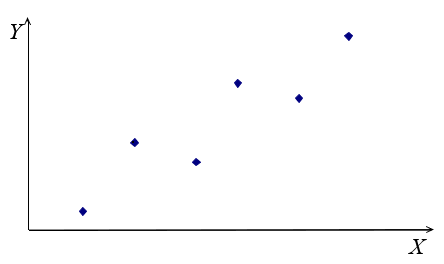
Lineaarset mudelit kirjeldab graafiliselt sirge \({\hat y_i} = \hat a{x_i} + \hat b\). Siin \( \hat a \) ja \(\hat b\) on mudeli parameetrite a ja b hinnangud, mis meil tuleb leida. \(\hat y_i \) on i-nda punkti koordinaadile xi vastava sirgel oleva punkti y-koordinaat ehk silutud väärtus. Seega tuleb meil leida seda punktiparve läbiva parima sirge võrrand. Aga läbi punktiparve võib tõmmata palju sirgeid. Näitena toodud kolm sirget: roheline, punane ja sinine.
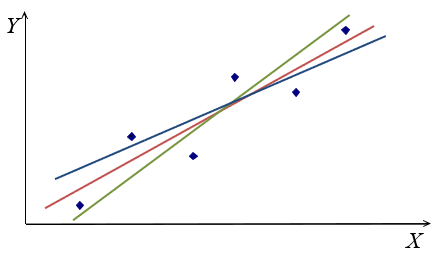
Milline neist kirjeldab seda punktiparve kõige paremini? Vaja on objektiivset arvulist kriteeriumi!
Sellise kriteeriumi leidmiseks leitakse kõigepealt silutud väärtuste \(\hat y_i \) erinevus vaatlusandmetest \(y_i\) mis on hälbed ehk jäägid (residuals):
\({u_i} = {y_i} - {\hat y_i}\)
Järgmisel diagrammil on kujutatud i-nda punkti jääk ühe väljavalitud sirge korral.
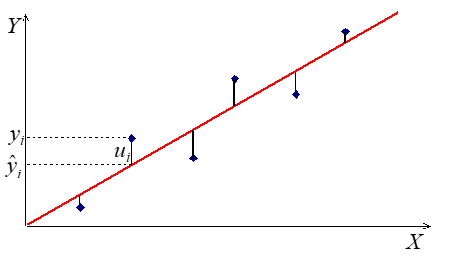
Kui meil on n punkti, saame ka n jääki. Kriteeriumiks on vaja aga üht suurust. Selleks sobib jääkide ruutude summa \(\sum\limits_{i = 1}^n {u_i^2} \).
Vähimruutude meetod: regressioonmudeli parameetrite hinnangud leitakse nii, et jääkide ruutude summa on minimaalne.
\(\sum\limits_{i = 1}^n {u_i^2} \; \to \;\min \)Nüüd on meil olemas arvuline kriteerium, mille abil saame võrrelda erinevaid sirgeid. Järgmises demos on samuti antud üks punktiparv ning saad proovida erinevaid sirgeid ning nende võrdlemiseks kasutada hälvete ruutude summat. Proovi leida selline sirge, mille korral hälvete ruutude summa on minimaalne.
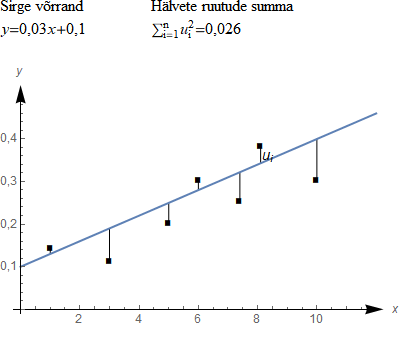
Demos said ka võrrelda enda poolt valitud sirget parima sirgega, mille parameetrid leiti valemite abil. Sirgete võrdlemise antud kriteeriumi järgi võib ju usaldada arvutile. Aga kuna läbi punktiparve võib tõmmata lõpmata palju sirgeid, siis ka ülikiirel arvutil kulub parima sirge leidmiseks lõpmata palju aega. On lihtsam tee: kasutada parameetrite a ja b hinnangute leidmiseks valemeid.
Kuidas nende valemiteni jõutakse? Hälbed võime avaldada tundmatute \(\hat a\) ja \(\hat b\) kaudu:
\({u_i} = {y_i} - {\hat y_i} = y_i-(\hat a x_i +\hat b) = {y_i} - \hat a{x_i} - \hat b\)
Meil tuleb minimeerida hälvete ruutude summat RSS ( Residual Sum of Squares)
\(RSS(\hat a,\hat b) = \sum\limits_{i = 1}^n {u_i^2} \; = {\sum\limits_{i = 1}^n {\left( {{y_i} - \hat a{x_i} - \hat b} \right)} ^2}\; \to \;\min \)
See tähendab, et tuleb leida kahe muutuja funktsiooni \(RSS(\hat a,\hat b)\) miinimumkoht. Matemaatilisest analüüsist on teada, et selleks tuleb I järku osatuletised panna võrduma nulliga
Seejärel tuleb lahendada saadud võrrandsüsteem. Lahendus on toodud näiteks Statistika õpikus (Sauga) lisas A.9. Valemid lineaarse mudeli parameetrite leidmiseks on
Neid valemeid kasutavad kõik statistika ja ökonomeetria paketid, kus on olemas vähimruutude meetod.
On võimalik näidata (Gauss-Markovi teoreem), et sel moel leitud hinnangud on
- nihketa;
- efektiivsed, so vähima dispersiooniga kõigi nihketa lineaarsete hinnangute seas;
- lineaarsed vaatluste yi suhtes
KUI kehtivad klassikalise lineaarse mudeli eeldused.
Kui CLRM (Classical Linear Regression Model) eeldused on täidetud, annab vähimruutude meetod parima lineaarse nihketa hinnangu BLUE (Best Linear Unbiased Estimator).
Eelnevalt oli meil soov leida Houthakkeri andmeid kasutades mudel, mis kirjeldab elektrienergia tarbimise sõltuvust tarbija sissetulekust Suurbritannia linnades. Mudelit otsime kujul \({y_i} = b + a{x_i} + {u_i}\), kus y on elektrienergia tarbimine (kWh aastas) ja x elanike sissetulek (GBP aastas). Regressioonmudeli hindamise aruande esimene osa programmis Gretl näeb välja selline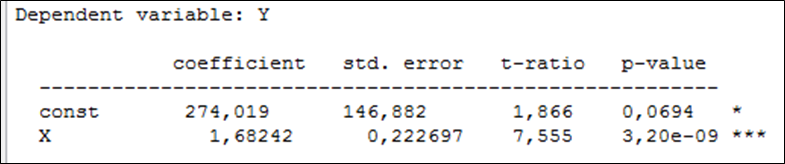
Veerus coefficient on parameetrite hinnangud: konstant ehk vabaliige ja tunnuse x kordaja. Järelikult
parameetri b hinnang \(\hat b \approx 274\);
parameetri a hinnang \(\hat a \approx 1,68\)
ning mudel \({y_i} = 274 + 1,68{x_i} + {u_i}\).
Regressioonmudeli aruande struktuur on ühesugune kõigis statistika- ja ökonomeetriapakettides. Gretli aruande põhjaliku selgitusega võib tutvuda siin. Enamike aruandes toodud suurustega tutvume selle ja järgmiste teemade juures.
4. Lineaarse mudeli tõlgendamine
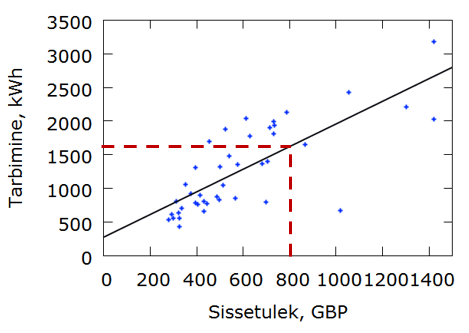
Eelmises peatükis jõudsime mudelini, mis kirjeldab elektrienergia tarbimise sõltuvust elanike sissetulekust Suurbritannia linnades. Seda mudelit võime nüüd kasutada arvutusteks. Näiteks mingis linnas oli elanike keskmine sissetulek 800 GBP aastas. Kui suur oli seal keskmine elektrienergia tarbimine pere kohta?
Mudeliks saime \({\hat y_i} = 274 + 1,68{x_i}\), kus y on elektrienergia tarbimine (kWh aastas) ja x elanike sissetulek (GBP aastas). Kui meid huvitab keskmine tarbimine linnas, kus keskmine sissetulek on 800 GBP, paneme arvu 800 mudelisse ja arvutame välja:
\({\hat y_i} = 274 + 1,68 \cdot 800 = 1618\) kWh aastas.
See on silutud väärtus ehk mudelväärtus.
Mingi konkreetse pere tegelik tarbimine on
Kasutades tingliku keskväärtuse mõistet, siis 1618 kWh on kõigi selliste perede, kellel sissetulek 800 GBP, elektritarbimise keskväärtus.
Nii võime mudelit kasutada prognooside tegemiseks. Aga palju olulisem on osata tõlgendada mudeli parameetreid. Need pole lihtsalt arvud, vaid neil on oma majanduslik sisu.
Tuletame kõigepealt meelde lineaarse mudeli
y=ax+b
parameetrite tõlgenduse üldjuhul.
Mudelist on näha, et kui x=0, siis y = b. Seega vabaliige b näitab y väärtust, kui x=0. See on puht matemaatiline tõlgendus. Reaalseid majandusprotsesse kirjeldavate mudelite korral pole see tõlgendus alati realistlik.
Olulisem on sirge tõusu ehk parameetri a tõlgendus. Kuidas selleni jõuda? Olgu meil mingi x väärtus x1 . Sellele vastav y väärtus on
y1 = a x1 + b
Mis juhtub, kui x1 suureneb 1 võrra? Milline on uus y väärtus?
y2 = a (x1 +1)+ b = a x1 +a + b = a x1 +b + a =y1 +a
Näeme, et y muutub a võrra. Järelikult kordaja a näitab, kui palju muutub y, kui x suureneb ühiku võrra.
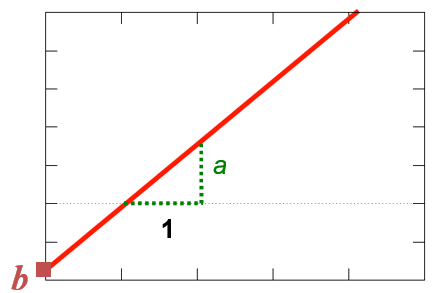
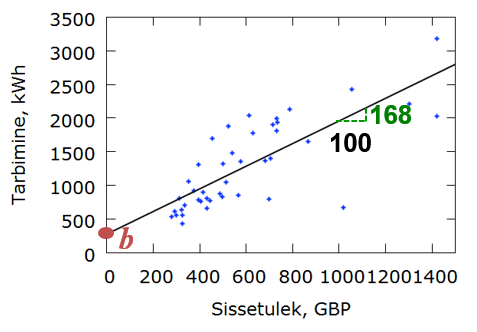
Mudelist \({\hat y_i} = 274 + 1,68{x_i}\) näeme, et kui sissetulek on ühiku ehk 1 GBP võrra suurem, siis elektrienergia tabimine on 1,68 kWh suurem. Järelikult, kui sissetulek on 100 GBP võrra suurem, on tarbimine aastas 168 kWh võrra suurem.
Parameetri b ehk vabaliikme tõlgendus selle mudeli korral: kui sissetulek on 0, on tarbimine 274 kWh. Tõsi, see ei pruugi olla õige hinnang, sest sissetuleku väärtuse 0 lähedal meil andmed puuduvad ja seal võib mudeli kuju olla teistsugune.
Järgmises näites võrdleme tõusuparameetreid erinevate tarbimismudelite korral. Tarbimismudel näitab, kuidas majapidamise kulud mingile hüvisele sõltuvad kogukuludest. Kasutame Eesti leibkonnaeelarve uuringu andmeid aastast 2012.
X kulud kokku pereliikme kohta aastas (eurot).
Y kulud teatud hüvise (toit, transport, side) tarbimisele, pereliikme kohta aastas (eurot).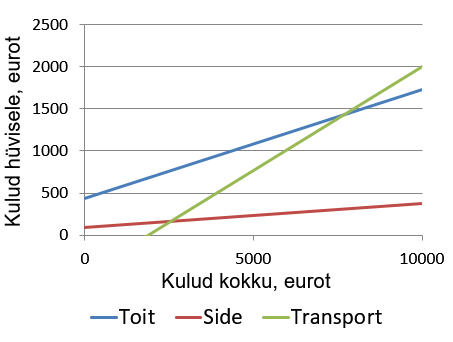
Toit: y = 434 + 0,13x + u
Transport: y= -464 +0,247x+u
Side: y= 97 + 0,0277x + u
Näeme, et kõige kiiremini kasvavad kulud transpordile. Kui kulud kokku suurenevad 1 euro võrra aastas, siis kulud transpordile suurenevad 0,247 eurot aastas. Ehk, kui kulud kokku suurenevad 1000 eurot aastas, siis kulud transpordile suurenevad 247 eurot aastas. See tähendab, et 24,7% kogukulude suurenemisest läheb transpordikulude suurendamisele.Kuidas aga tõlgendada trasnpordikulude mudelis olevat negatiivset vabaliiget? Kulud ei saa ju olla negatiivsed! Ei olegi. Esitame lihtsalt küsimuse: millal tekivad kulud transpordile? Siis, kui kogukulud pereliikme kohta on ca 1880 eurot aastas. Kuidas selleni jõuti?
Paneme kirja transpordikulude mudelväärtuse
\(\hat y = - 464 + 0,247x\)
Nüüd leiame, millise x väärtuse korral \(\hat y =0\), st lahendame võrrandi.
$$\begin{array}{rl}0 &= - 464 + 0,247x\\ - 0,247x &= - 464\\0,247x &= 464\\x &= \frac{{464}}{{0,247}} = 1878,54 \approx 1880\end{array}$$
Nii tõlgendatakse negatiivset vabaliiget, kui sõltuv tunnus y ei saa omada negatiivseid väärtusi: leitakse x selline väärtus, millest alates on y positiivne.
Testi ennast, kas oskad lineaarset mudelit tõlgendada.
5. Parameetrite standardvead
Vähimruutude meetodi rakendamisel leitakse lisaks parameetrite punkthinnangutele ka mudeli standardvea ja parameetrite standardvigade hinnangud. Nende põhjal saab leida parameetrite usalduspiirid ja mis veel olulisem, saab leida testimiseks vajalikud t-statistikud.
Vähimruutude meetodi kasutamisel minimeeritakse jääkide ruutude summat \(\sum\limits_{i = 1}^n {u_i^2} \) ja tulemuseks on mingi arv. Selle jagamisel vabadusastmete arvuga n-k , kus n on valimi maht ja k mudeli parameetrite arv, saadakse mudeli dispersiooni hinnang
\({s^2} = \frac{{\sum\limits_{i = 1}^n {u_i^2} }}{{n - k}} = \frac{{\sum\limits_{i = 1}^n {{{\left( {{y_i} - \hat a{x_i} - \hat b} \right)}^2}} }}{{n - k}}\)
Ruutjuur sellest on mudeli standardviga (standard error of regression)
\(se = \sqrt {{s^2}} \)
Parameetrite standardvead leitakse mudeli standardvea põhjal
\(se(\hat b) = se\sqrt {\frac{1}{n} + \frac{{{{\bar x}^2}}}{{\sum {{{\left( {{x_i} - \bar x} \right)}^2}} }}} \)
\(se(\hat a) = \frac{{se}}{{\sqrt {\sum {{{\left( {{x_i} - \bar x} \right)}^2}} } }}\)
Näitena vaatame elektrienergia tarbimise mudeli täielikku aruannet programmis Gretl.
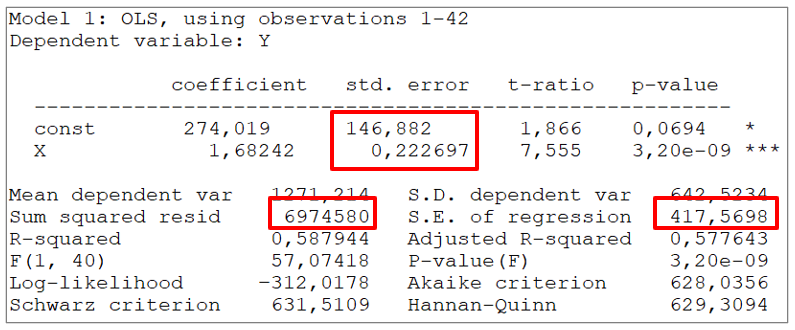
Jääkliikmete ruutude summa (Sum squared resid) on 6974580. Valimi maht on 42 ja mudeli parameetrite arv 2. Mudeli standardviga (S.E. of regression) on siis
\(se = \sqrt {\frac{{\sum\limits_{i = 1}^n {u_i^2} }}{{n - 2}}} = \sqrt {\frac{{6974580}}{{42 - 2}}} \approx 417,5698\)
Kui nüüd leida \(\bar x ^2= 351310\) ja \(\sum {\left( x_i - \bar x \right)^2} =3515822\), mis aruandes pole kuvatud, siis parameetrite standardvead
\(se(b) = se\sqrt {\frac{1}{n} + \frac{{{{\bar x}^2}}}{{\sum {{{\left( {{x_i} - \bar x} \right)}^2}} }}} =417,6598 \sqrt{\frac {1}{42} + \frac{ 351310}{3515822}} =146,882\)
\(se(a) = \frac{{se}}{{\sqrt {\sum {{{\left( {{x_i} - \bar x} \right)}^2}} } }} = \frac{{417,5698}}{{\sqrt {3515822} }} = 0,222697\)
Parameetrite standardvead on aruande tabeli veerus std. error ja loomulikult ei pea me neid ise arvutama. Aga peame aru saama nende arvutusvalemitest, sest see võimaldab vaatlusi paremini organiseerida. Kui vaatame veelkord parameetri a standardvea valemit, siis nimetajas on \(\sum {\left( x_i - \bar x \right)^2} \), mis isleoomustab tunnuse x väärtuste hajumist ümber aritmeetilise keskmise. Kui see hajumine on väike, st nimetaja on väike, siis murd on suur. Järelikult, kui x väärtused hajuvad vähe, tuleb parameetri standardviga suur. Sama kehtib ka parameetri b standardvea kohta.
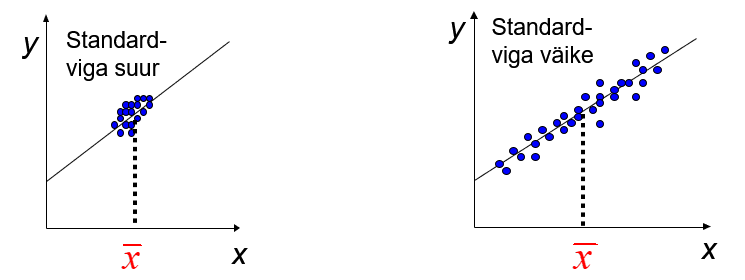
Täpsemate hinnangute saamiseks peavad tunnuse x väärtused võimalikult palju hajuma. Seda peab silmas pidama valimi moodustamisel.
Parameetrite hinnangute usalduspiiride leidmisel lähtutakse sellest, et hinnangute standardiseeritud erinevused tegelikest väärtustest alluvad t jaotusele vabadusastmete arvuga \(\nu = n - k\), kus n on valimi maht ja k parameetrite arv mudelis (hariliku lineaarse mudeli korral k=2):
\(\frac{{\hat a - a}}{{se(\hat a)}} \sim t(\nu )\quad ,\quad \frac{{\hat b - b}}{{se(\hat b)}} \sim t(\nu )\)
\(\hat a \pm t_{\alpha /2}\,(\nu ) se(\hat a) \;\;\; \hat b \pm t_{\alpha /2}\,(\nu ) se(\hat b)\)
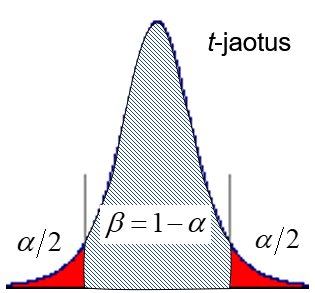
Viirutatud ala on tõenäosus, et parameetri tegelik väärtus jääb usalduspiiridesse. Punane ala: tõenäosus, et tegelik väärtus on väljaspool usalduspiire.
See, et mudeli parameetrite hinnangud ei vasta täpselt tegelikele väärtustele, vaid tegelikud väärtused jäävad usaldatavusega β usalduspiiridesse, tähendab, et valimi põhjal leitud regressioonsirge ei vasta täpselt tegelikule sirgele. Tegelik sirge jääb teatud veakoridori. Joonisel on tootud eraldi kummagi parameetri määramatusest ning mõlema parameetri määramatusest tingitud sirge asendi määramatus.
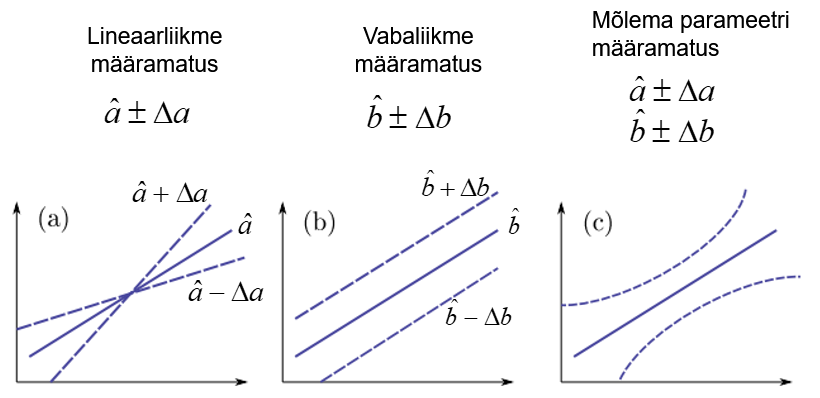
Tabelarvusprogrammis Excel kuvatakse parameetrite usalduspiirid regressioonmudeli hindamise aruande viimastes veergudes. Ökonomeetria pakettide aruannetes parameetrite usalduspiire tavaliselt ei kuvata, kuid neid saab eraldi vaadata. Programmis Gretl näiteks preale mudeli hindamist Analysis->Confidence intervals for coefficients. Järgnevalt on esitatud Houthakkeri elektrienergia tarbimise mudeli parameetrite usalduspiirid usaldatavusega 95%.

Siit näeme, et kui aastane sissetulek x suureneb ühiku ehk 1 GBP võrra, siis elektrienergia tarbimise suurenemine jääb tõenäosusega 95% vahemikku 1,23 kuni 2,13 kWh aastas. Näeme ka seda, et kui sissetulek puudub (x=0), siis tarbimine võib olla 0 kWh, sest 0 jääb konstandi usaldusvahemiku sisse.
6. Parameetrite testimine
Uurime, kas võib eksisteerida seos riigi peaministri nime ja riigi SKP vahel. Kasutades 2012. a andmeid 7 riigi kohta (Eesti, Läti, Leedu, Soome, Rootsi, Taani, Norra), saame mudeliks
\(\widehat {SKP} = 15n - 54,7\)
kus SKP on miljardites eurodes ja n peaministri täisnimes olevate tähtede arv. Andmeid võib vaadata Statistika õpikust (Sauga) lk 465 näide 9.14.
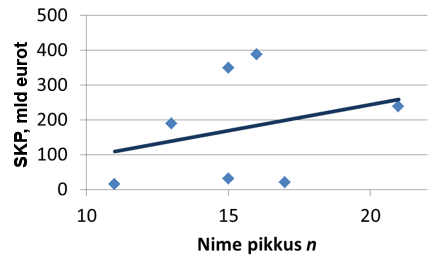
Kas me võime saadud mudeli põhjal väita, et kui riigi peaministri nimi on pikem, on ka riigi SKP suurem? Et iga täht peaministri nimes suurendab riigi SKP-d ligikaudu 15 mld euro võrra? Vaevalt selline järeldus usaldusväärne on.
Siit tuleb vajadus testida parameetrite statistilist olulisust. Vähimruutude metodil saab leida parima sirge läbi suvalise punktiparve. Ka siis, kui need punktid on juhuslikult hajunud ning seos X ja Y vahel puudub. Usaldada võime ainult neid parameetrite hinnanguid, mis on statistiliselt olulised. Kõige sagedamini on regressioonmudeli korral vaja testida, kas tunnused Y ja X on omavahel seotud, st kas tõusuparameeter a erineb oluliselt nullist.
Testimiseks kasutatakse t-statistikut, mis on parameetri hinnangu ja standardvea suhe:
\(t = \frac{{\hat a - 0}}{{se(\hat a)}} = \frac{{\hat a}}{{se(\hat a)}}\)
Tegemist on kahepoolse hüpoteesiga.
Nullhüpotees H0 \(a=0\)
Sisukas hüpotees H1 \(a \neq 0\)
Kriitiline piirkond (vastu võtta H1): \(|t| > t_{\alpha/2}(\nu )\) ehk p < α
See on parameetrite statistilise olulisuse testimine. Kui nullhüpotees on ümber lükatud (võetakse vastu sisukas hüpotees), on parameeter oluliselt nullist erinev, järelikult seos on olemas. Kui tuleb vastu võtta nullhüpotees, siis pole seose olemasolu tõestatud.
Järgmises demos saad harjutada regressioonmudeli parameetri statistilise olulisuse testimist ning näed, kuidas tulemust mõjutab valimi maht, parameetri punkthinnang, parameetri standardviga ja ette võetud olulisuse nivoo α.
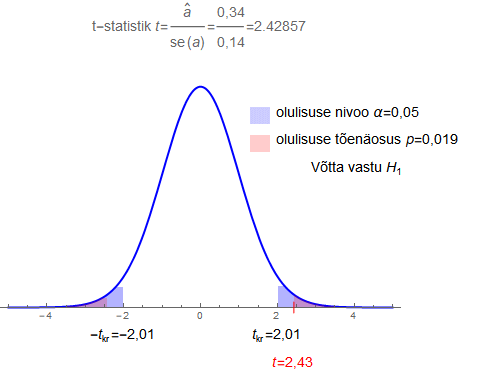
Demos nägid, kuidas mõjutavad hüpoteesi testimise tulemust erinevad näitajad.
Testi ennast, kas said demost õigesti aru.
Regressioonmudeli aruandes kuvatakse iga parameetri jaoks nii t-statistiku väärtus kui ka sellele vastav olulisuse tõenäosus p. Otsuse vastuvõtmiseks on kõige lihtsam võrrelda olulisuse tõenäosust p olulisuse nivooga α (tavaliselt 0,05).
- Kui p >α, võtta vastu nullhüpotees, st parameeter pole statistiliselt oluline.
- Kui p < α, võtta vastu sisukas hüpotees, st parameeter on statistiliselt oluline.
Riigi SKP ja peaministri nimes olevate tähtede arvu n vahelise seose hindamise aruanne on järgmine

\(t=\frac{14,9553}{21,3950}=0,699\)
Veerus p-value on neile t-statistikutele vastavad olulisuse tõenäosused, mis on leitud t-jaotusest. Nagu näeme, on mõlemad oluliselt suuremad kui 0,05, seega mõlemad parameetrid on statistiliselt mitteolulised ja seda mudelit usaldada ei saa.
Kui me aga vaatame elektrienergia tarbimise mudeli aruannet, siis näeme, et sissetuleku X ees oleva kordaja olulisuse tõenäosus on 3,2·10-9 < 0,05 ning võtame vastu sisuka hüpoteesi. On tõestatud, et sissetuleku X ja elektrienergia tarbimise Y vahel on seos.
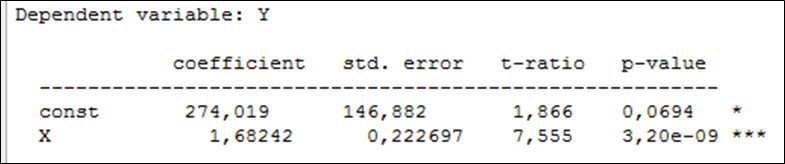
Seega enne, kui me hakkame vaatama parameetrite hinnanguid (veerg coefficient), tuleb vaadata olulisuse tõenäosusi veerus p-value, et teha kindlaks, kas parameetrite hinnangud on usaldusväärsed. Kui parameetrid on statistiliselt olulised, alles siis on mõtet vaadata hinnangute arvväärtusi, tõlgendada neid ja mudelit tervikuna.
Regressioonmudeli aruandes kuvatakse automaatselt info parameetri statistilise olulisuse testimise kohta, st testitakse, kas parameeter erineb oluliselt nullist. Aga mõnikord on statistiliselt olulise parameetri korral lisaks vaja testida, kas parameetri hinnang on oluliselt erinev mõnest muust arvust.
Näiteks finantsvarade hindamise mudeli CAPM (Capital Asset Pricing Model) üldkuju on järgmine
INV = β TP + u
Siin
INV = R - RF
TP = RM - RF
kus R on investeeringu oodatav tulumäär, RF riskivaba tulumäär antud turul (näiteks riigi võlakirjade tulusus) ja RM turuportfelli tulusus. Turuportfell esindab kõiki turul ringlevaid väärtpabereid.
Kordaja β on investeeringu süstemaatilise riski mõõt ehk beetakordaja. CAPM mudeli hindamisel kasutatakse tulumäärade aegridu ja leitakse beetakordaja. Kui β > 1, on tegemist agressiivse investeeringuga: investeeringu tulumäära liikumine on suurem kui turuportfellil, investeeringu risk on turu keskmisest kõrgem. Seega CAPM mudeli beetakordajat peab võrdlema arvuga 1 ja tuleb testida hüpoteesipaari
H0: β ≤ 1
H1: β > 1
Sellisel testimisel tuleb mudeli aruande põhjal arvutada teststatistik ja võrrelda seda kriitilisega. Teststatistiku valem üldjuhul
\(t = \frac{{\hat a - {a_0}}}{{se(\hat a)}}\),
kus \(\hat a\) on parameetri hinnang, \(a_0\) nullhüpoteesile vastav parameetri väärtus ja \(se(\hat a)\) parameetri hinnangu standardviga. Parameetri hinnang ja selle standardviga võetakse mudeli hindamise aruandest.
| Kahepoolne | Ühepoolne | |
|---|---|---|
| Nullhüpotees H0 | a=a0 | a ≤ a0 a ≥ a0 |
| Sisukas hüpotees H1 | a≠a0 | a > a0 a< a0 |
| Kriitiline piirkond (võtta vastu H1) | |t|> tα/2 (υ) p < α |
|t|> tα (υ) p < 2α |
Vabadusastmete arv υ= n -k, kus n on valimi maht ja k mudeli parameetrite arv.
7. Determinatsioonikordaja
Kui mudeli parameetrid on statistiliselt olulised, tuleb hinnata ka mudeli kirjeldusvõimet. Alljärgneval joonisel on regressioonjooned kahe erineva punktiparve korral.
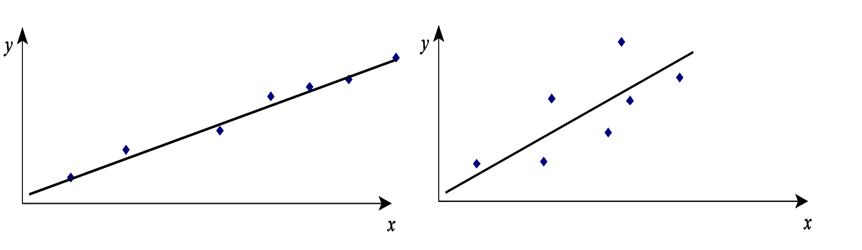
Vasakpoolsel joonisel on mudeli kirjeldusvõime suurem kui parempoolsel joonisel. Aga kuidas kirjeldusvõimet kvantitatiivselt hinnata? Selleks kasutatakse determinatsioonikordajat R2 (R-square).
Determinatsioonikordaja leidmiseks analüüsitakse sõltuva tunnuse Y hajuvust. Eristatakse koguhajuvust, jääkhajuvust ja seletatud hajuvust.
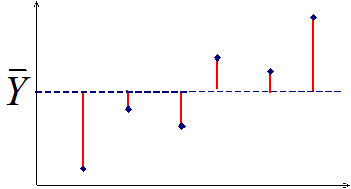
| Koguhajuvus (Total Sum of Squares) iseloomustab sõltuva tunnuse väärtuste hajumist ümber selle keskväärtuse ja selle kvantitatiivseks hindamiseks kasutatakse hälbeid keskväärtusest: \(TSS = \sum {{{\left( {{y_i} - \bar y} \right)}^2}} \) |
|
| Jääkhajuvus (Residual Sum of Square) siseloomustab sõltuva tunnuse väärtuste hajumist ümber regressioonjoone ja selle kvantitatiivseks hindamiseks kasutatakse hälbeid regressioonjoonest: \(RSS = \sum {{{\left( {{y_i} - \hat y} \right)}^2}} \) |
 |
Regressioonmudeliga kirjeldatud hajuvus ehk seletatud hajuvus (Explained Sum of Squares) on nende vahe:
\(ESS = TSS-RSS\)
Determinatsioonikordaja näitab, kui suur osa koguhajuvusest on mudeli poolt ära seletatud
\({R^2} = \frac{{{\rm{seletatud \; hajuvus}}}}{{{\rm{koguhajuvus}}}} = \frac{{ESS}}{{TSS}} = 1 - \frac{{RSS}}{{TSS}}\)
Loomulikult ei saa seletatud hajuvus olla suurem kui koguhajuvus, järelikult 0< R2 <1. Tihti esitatakse determinatsioonikordaja protsentides.
Järgmises demos saad muuta punktide hajuvust ümber sirge ja jälgida, kuidas muutub determinatsioonikordaja väärtus.
Regressioonmudeli aruandes kuvatakse determinatsioonikordaja väärtus. Näitena toodud elektrienergia tarbimise mudeli aruanne.
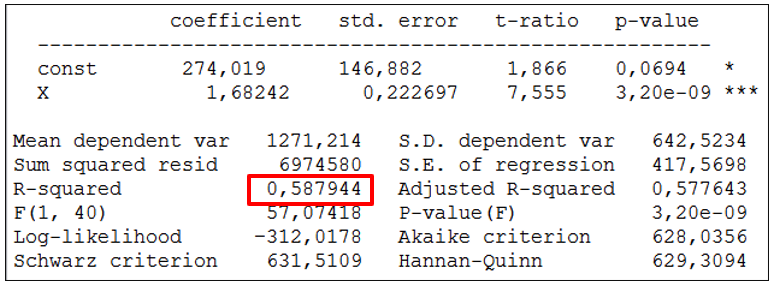
Sissetuleku varieerumine seletab ära ca 58,8% elektrienergia tarbimise varieerumisest. Koguhajuvust, seletamata ja seletatud hajuvust iseloomustavad näitajad on esitatud ANOVA tabelis (programmis Gretl mudeli aruiandes Analysis->ANOVA)

Punasega on aruandele lisatud eespool toodud näitajate tähistused. Aruandes on esitatud on ka determinatsioonikordaja R2 arvutus ESS/TSS.
Hariliku lineaarse regressioonmudeli y=ax+b+u korral on determinatsioonikordaja võrdne lineaarse korrelatsioonikordaja r ruuduga
\(R^2 = r^2\)
Determinatsioonikordaja sisu on paremini mõistetav kui korrelatsioonikordaja oma.
8. Mudeli korrektne esitamine
Regressioonanalüüsi põhitulemuste esitamisel esitatakse
- parameetrite hinnangud;
- parameetrite
standardvead;
- determinatsioonikordaja
R2;
- valimi
maht n.
\(\begin{array}{l}y = \hat b\quad + \quad \hat a\,\;x + u\quad \quad {R^2} = ...\\\;(se(b))\;\quad (se(a))\;\quad \quad n = ...\end{array}\)
Näitena elektrienergia tarbimise mudeli korrektne esitus, mis on saadud mudeli aruande põhjal.
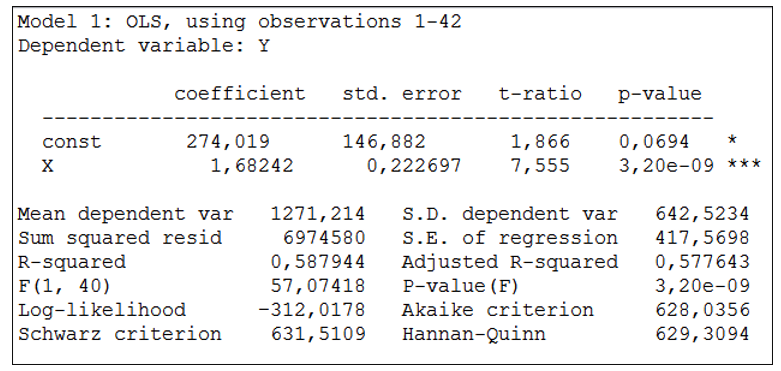
\(\begin{array}{l}{y_i} = 274 + 1,68\,{x_i} + {u_i}\quad \quad {R^2} = 0,588\\\;\quad (147)\;(0,22)\quad \quad \quad \quad \;n = 42\end{array}\)
kus x on majapidamise sissetulek aastas (GBP) ja y elektrienergia tarbimine aastas (kWh).
Tingimata tuleb lisada kasutatud tähistuste seletused koos ühikutega. Kui me ei lisa tähistuste seletusi, pole mudelist mingit kasu, sest keegi ei saa sellest aru. Ja kui me ei lisa ühikuid, ka siis pole võimalik mudelit korrektselt tõlgendada.
Tähele tuleb panna seda, et arvud ümardatakse sobivalt. Standardviga esitatakse kas kahe või kolme tüvenumbriga, parameetri hinnang ümardatakse vastavalt vea teise või kolmanda tüvenumbrini. Ülearuste numbrite esitamine on infomüra, sest kui näiteks viga on juba sajalistes, siis pole mingit mõtet esitada kohti peale koma. Nendel kohtadel olevad numbrid pole niikuinii usaldusväärsed ja segavad.
Nüüd oleme vaadanud läbi programmi Gretl regressioonmudeli aruandes esitatud kõige olulisemad näitajad.
Testi ennast, kas oskad mudeli aruandest leida vajalikud suurused.
Kasutades autotootja Audi AG 2014. aasta aruandest võetud andmeid aastate 2005 kuni 2014 kohta, on hinnatud kulufunktsiooni kujul C=aq+b+u, kus C on kulud miljardites eurodes ja q aastas toodetud autode arv tuhandetes ehk tootmismaht. Mudeli hindamise aruanne:
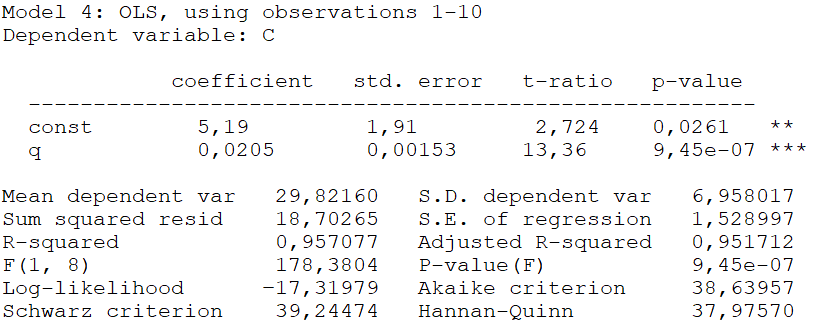
9. Erindi mõju
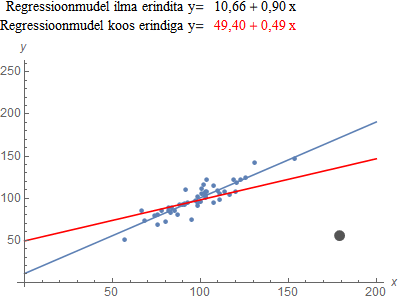
Erindiks nimetatakse sellist vaatlust, mis asub teistest väga kaugel. Üks erind võib oluliselt mõjutada regressioonmudeli parameetreid.
Järgnevas demos saad ühe vaatluse teistest eemaldada ja vaadata, kuidas muutub regressioonjoone asend.
Kõige lihtsam meetod erindi(te) avastamiseks on uurida hajumisdiagrammi. Erindite avastamisel tuleb kaaluda mudeli hindamist ilma erinditeta. Neljanda teema juures tutvume ka ebaharilike vaatluste avastamisega sobivate kvantitatiivsete näitajate abil.
Kui seletava tunnuse x väärtused on väga suure asümmeetriaga, siis ka see näitab, et eksisteerib ekstreemseid väärtusi. Sellisel juhul tavaliselt seda tunnust logaritmitakse, et vähendada ekstreemsete väärtuste mõju. Logaritmimisel muutub jaotus sümmeetrilisemaks.
Näiteks õpikus Wooldrige, (2002) "Introductory Econometrics: A Modern Approach" analüüsiti 209 ettevõtte andmeid aastal 1990. Andmed võeti ajalehest "Businessweek". Üheks näitajaks oli ettevõtte müügikäive (sales) aastas (mln $). Vasakpoolsel joonisel on käibe jaotushistogramm. Nagu näha, esineb väike arv ettevõtteid, mille käive on teistega võrreldes väga suur. 95% ettevõtetest jäi käive alla 21 mld dollari, aga 10 ettevõttel oli see suurem. Ühel ettevõttel lausa 98 mld $. Asümmeetriakordaja on 5.
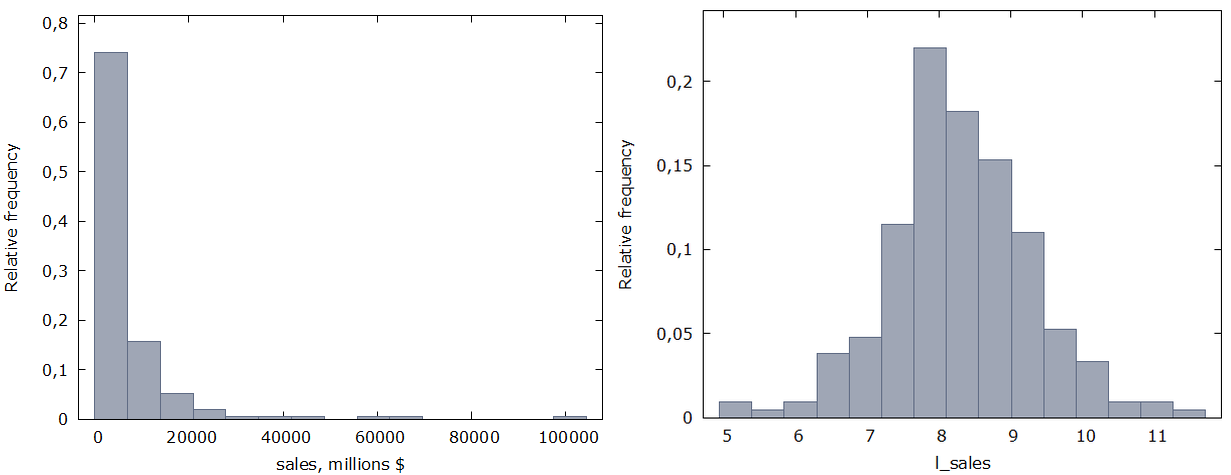
Parempoolsel diagrammil on aga logaritmitud käive, st on leitud käibe naturaallogaritm. Nagu näha, on jaotus üsna sümmeetriline. Asümmeetriakordaja on 0,1. Seega regressioonmudelisse tuleks panna logaritmitud käive.
10. Vabaliikme olemasolu
Hariliku lineaarse regressioonmudeli \(y_i=ax_i+b+u_i\) parameetrit b nimetatakse eesti keeles vabaliikmeks. Inglise keeles kasutatakse tähistust const, mis tähendab, et see liidetav on mudelis konstantne. Ülejäänud liidetavad on erinevatel objektidel erinevad, sest xija ui on erinevatel objektidel erinevad.
Vabaliikme statistilist olulisust regressioonmudelis üldiselt ei vaadata. Kui ka vabaliige on statistiliselt mitteoluline, ilma vabaliikmeta mudelit üldiselt ei kasutata. Vabaliikme olemasolu on vajalik vähimruutude meetodi rakendamise seisukohalt. Vabaliige garanteerib, et regressioonijääkide summa
\(\sum\limits_i {{u_i}} = 0\)
Mitmete regressioonanalüüsi käigus leitavate suuruste valemite (nt determinatsioonikordaja) tuletamisel kasutatakse seda omadust.
Mõnikord tuleb siiski hinnata lineaarset mudelit, kus teatud kaalutlustest lähtudes peab vabaliige puuduma. Seda nimetatakse regressiooniks läbi nullpunkti (Regression Through the Origin, RTO) ja sellise mudeli üldkuju ühe seletava tunnuse korral on
\(y=ax+u\)
See tähendab, et mudeli deterministlik komponent on võrdeline seos \(\hat y = ax\). Näiteks \( \hat y=2x\)
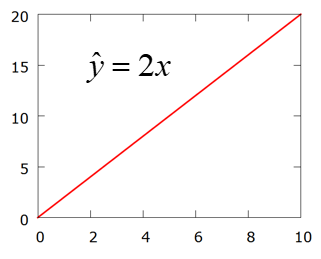
Regressioonjoont läbi nullpunkti kasutatakse näiteks peatükis 6 vaadeldud finantsvarade hindamise CAPM mudelis INV = β TP + u.
Üks näide sellise mudeli kohta. Ajakirjas Journal of Environmental Horticulture 2006. aastal ilmunud artiklis (Lu, W. et al) analüüsiti, kuidas puukoore tootmine sõltub metsaraie mahust. Kasutati andmeid USA erinevatest piirkondadest aastatel 1986-2001. Kui metsa ei raiuta, siis puukoort turule ei tule. See tähendab, et kui raiemaht on 0, siis ka puukoore tootmine on 0. Seepärast kasutati ilma vabaliikmeta lineaarset mudelit
y=ax+u,
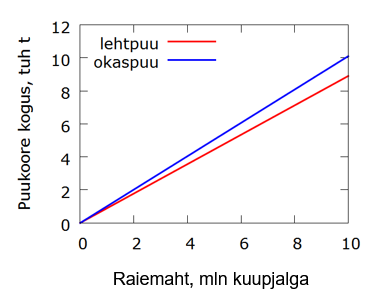
kus y on kuiva puukoore kogus (tuh tonni) ja x raiemaht antud piirkonnas (mln kuupjalga). USA kirdeosa jaoks saadi:
lehtpuu \(\hat y = 0,89x\)
okaspuu \(\hat y = 1,01x\)
- vabaliikmega mudelis on see statistiliselt mitteoluline;
- vabaliikme puudumine mudelist on teoreetiliselt põhjendatud.
11. Lineariseeritavad mudelid
Peatükis 9, kus vaadeldi erindi mõju, oli toodud näide 209 ettevõtte käibe jaotusest. See oli väga asümmeetriline, valimis esinesid üksikud ettevõtted, mille käive oli ülejäänud ettevõtetega võrreldes väga suur. Asümmeetria vähendamiseks käivet logaritmiti.
Vaatleme nüüd samade ettevõtete andmete põhjal koostatud regressioonmudelit, kus ettevõtte tegevjuhi palk (salary) sõltub ettevõtte käibest (sales). Palk on tuhandetes dollarites ja käive miljonites dollarites.
Kui kasutame lineaarset mudelit, siis mudeli hindamine annab
\(\widehat {{\rm{salary}}} = 0,015{\rm{sales}} +1174 \quad \quad \quad {R^2} = 0,015\) (1)
Mudeli kirjeldusvõime on väga madal. Hajumisdiagrammi analüüsimine näitab, et esinevad erindid. Diagrammilt on näha, et lisaks mõnele väga suure käibega ettevõttele on ka mõned sellised, kus käive on väike, aga tegevjuhi palk väga suur.
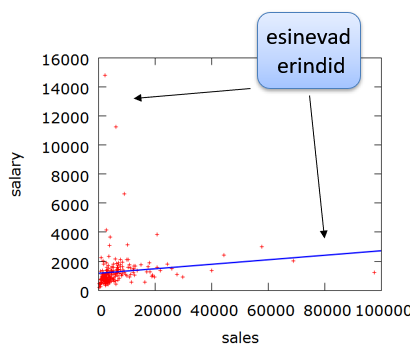
Logaritmime mõlemat tunnust. Mudelit, kus mõlemad tunnused on logaritmitud, nimetatakse log-log mudeliks. Tulemuseks on
\( \ln \widehat {{\rm{salary}}} = 0,257 \ln {\rm{sales}} +4,8 \quad \quad \quad {R^2} = 0,211\) (2)
Mudeli kirjeldusvõime tõusis. Hajumisdiagrammil erindeid enam ei esine.
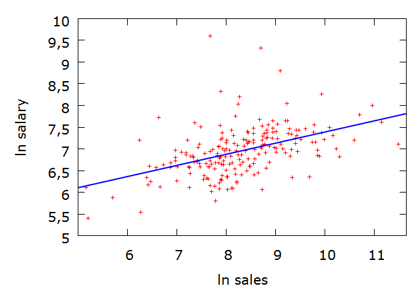
Järelikult log-log mudel kirjeldab seda seost oluliselt paremini.
Tuletame meelde, et lineaarse mudeli kordaja näitab, kui palju muutub y, kui x muutub 1 võrra. Seega lineaarne mudel (1) ütleb, et kui ettevõtte käive on 1 mln $ võrra suurem, siis ettevõtte juhi töötasu on 0,015 tuh $ võrra suurem.
Mida näitab aga log-log mudeli kordaja?
Log-log mudeli kordaja näitab, mitu % muutub Y, kui X suureneb 1%. Seega log-log mudeli kordaja on elastsuskordaja.
Toodud näites mudelist (2): kui ettevõtte käive on 1% suurem, siis ettevõtte juhi töötasu on 0,257% suurem.
Lineaarse mudeli ja log-log mudeli erinevus:
- lineaarne mudel: piirkalduvus (sirge tõus) on konstantne;
- log-log mudel: elastsuskordaja on konstantne.
Tuletame ühtlasi meelde, mis on elastsuskordaja. Elastsuskordaja E seob omavahel tunnuste x ja y suhtelisi muutusi:
\(\frac{\Delta y} {y} = E \frac {\Delta x}{x}\)
Kui avaldame sellest seosest E, siis
\(E = \frac {x}{y} \frac{\Delta y}{\Delta x}\)
Kui me tahame leida elastsuskordaja väärtust ühes punktis (punktelastsus), tuleb lõplikud muudud Δy ja Δx asendada lõpmatult väikeste muutudega ehk diferentsiaalidega dy ja dx:
\(E = \frac {x}{y}\frac{{dy}}{{dx}}\) (3)
kus \(\frac{{dy}}{{dx}}\) on y tuletis x järgi.
Kirjutame välja log-log mudeli üldkuju
\( \ln y= E \ln x +c +u \) (4)
Siit tuleb ka vajadus kasutada log-log mudelis naturaallogaritme. Kui rakendame elastsuskordaja arvutamise valemit (3) seosele (4), siis saame, et ln x ees olev kordaja on elastsuskordaja. Kui kasutaksime näiteks kümnendlogaritme, oleks elastsuskordaja leidmine mudeli parameetrite põhjal oluliselt keerulisem.
Tunnuste x ja y suhtes on mudel (4) mittelineaarne. Aga logaritmitud tunnuste suhtes on mudel lineaarne. Seda on lihtne näha, kui võtame kasutusele uued tähistused \(w=\ln y\) ja \(z= \ln x\). Siis saab log-log mudeli (4) kirja panna kujul
\(w= E z +c +u \)
ning on näha, et tunnuste w ja z suhtes on mudel lineaarne. Järelikult parameerite E ja c leidmiseks saab kasutada harilikku vähimruutude meetodit.
Vaatame ka üht teist mittelineaarset mudelit. Analüüsime USA SKP muutumist aastatel 1800 kuni 2009. SKP on miljardites dollarites.
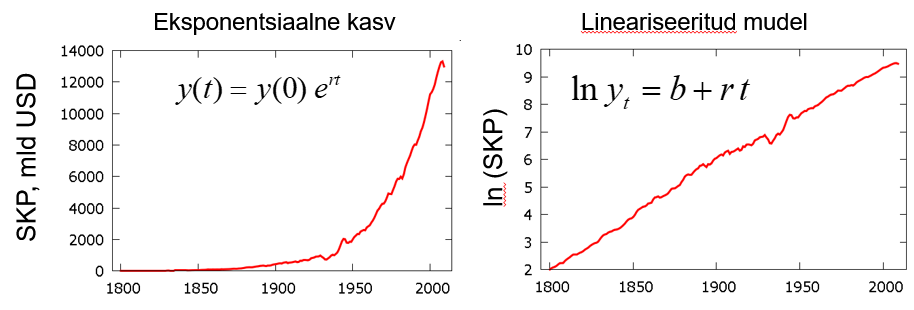
Vasakpoolsel diagrammil on esitatud SKP muutus ajas. Graafikult on näha, et tegemist on eksponentsiaalse kasvuga, mida kirjeldab mudel
\( y(t)=y(0) e^{rt}\), (5)
kus t on aeg aastates, t=1 aastal 1800. Põhimõtteliselt võib ajamuutuja defineerida ka nii, et vaadeldava perioodi alguses t=0, kuid ökonomeetriapakettides võetakse ajamuutuja esimeseks väärtuseks alati 1. Parameeter r on kasvumäär ja see näitab, mitu protsenti keskmiselt on SKP igal aastal kasvanud. See mudel on mittelineaarne ja kasvumäära r leidmiseks ei saa kasutada harilikku vähimruutude meetodit. Kui aga mudelit lineariseerida, saame aja t suhtes lineaarse mudeli. Parempoolsel diagrammil on näha, et suurus \(\ln y\) muutub ajas ligikaudu lineaarselt. Selle mudeli parameetreid on võimalik hinnata hariliku vähimruutude meetodi OLS abil. Sõltuva tunnuse logaritmimine teisendab eksponentsiaalse kõvera lineaarseks.
Toome ära eksponentsiaalse mudeli (5) lineariseerimise etapid, st millised matemaatilised teisendused tuleb teha.
\(y(t) = y(0){e^{rt}}\)
Logaritmime võrduse mõlemaid pooli
\(\ln y(t) = \ln \left( {y(0){e^{rt}}} \right)\)
Kasutame logaritmi omadust: korrutise logaritm on tegurite logaritmide summa
\(\ln y(t) = \ln y(0) + \ln {e^{rt}}\)
Teise liidetava juures arvestame seda, et \(\ln e ^{rt} = rt\). Sest naturaallogaritm näitab ju seda, millisele astmele tuleb arv e võtta, et saada logaritmi all olev avaldis, milleks antud juhul on \(e^{rt}\). Loomulikult astmele \(rt\).
\(\ln y(t) = \ln y(0) + rt\)
Võtame nüüd vabaliikme tähistamiseks kasutusele tähe b
\(b = \ln y(0)\) (6)
Saimegi aja t suhtes lineaarse mudeli
\(\ln y(t) = b + rt\) (7)
Sellist mudelit, kus sõltuv tunnus y on logaritmitud, aga seletav tunnus on mudelis lineaarselt, nimetatakse log-lin mudeliks.
Kasutades nüüd andmeid USA SKP kohta, hindame mudelit \(\ln {SKP_t} = r\,t + b + {u_t}\), kus SKP on miljardites dollarites ja t aeg aastates (t=1 aastal 1800). Mudeli hindamise aruanne on järgmine:
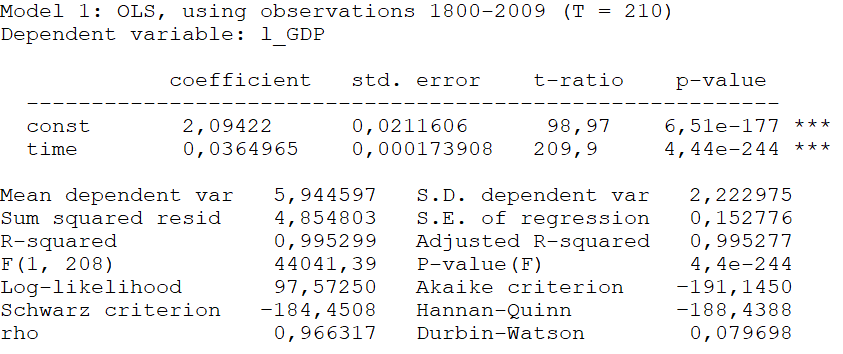
Näeme, et ajamuutuja time ees oleva kordaja (kasvumäära) olulisuse tõenäosus on 4,44·10-244 < 0,05, st kasvumäär on statistiliselt oluline. Paneme kirja saadud mudeli kujul (7)
\(\begin{array}{rccl}\ln {\widehat {SKP}_t} & = &2,094 + &0,03650t\quad \quad {R^2} = 0,995 \quad \quad T = 210\\& \;&(0,021)& (0,00017)\end{array}\)
USA SKP kasvumäär r on olnud keskmiselt 3,65% aastas.
Järgmisel diagrammil on logaritmitud SKP tegelikud väärtused (punane joon) ja mudelväärtused (sinine).
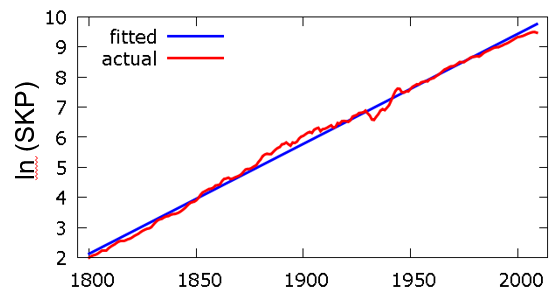
Teades kasvumäära r, võime kirja panna ka SKP kasvu mudeli eksponentsiaalsel kujul (5). Selleks tuleb aga enne arvutada eksponentsiaalses mudelis olev konstant y(0). Selle saame leida, kui arvestame eksponentsiaalse mudeli lineariseerimisel kasutusele võetud tähistust lineaarse mudeli vabaliikme kohta (6). Kuna b väärtus on regressioonanalüüsi abil hinnatud, b= 2,094, siis
\(y(0)= e^{2,094} \approx 8,12\)
Nüüd SKP kasvu mudel eksponentsiaalsel kujul
\(\widehat{SKP}=8,12 e^{0,0365t}\),
kus SKP on miljardites dollarites ja t aastates, t=1 aastal 1800.
Seda mudelit võime kasutada ka prognoosimiseks, eeldades, et keskmine kasvumäär on konstantne. Leiame mudeli järgi SKP väärtuse aastal 2019. Siis t=220. Paneme selle mudelisse ja arvutame välja:
\(\widehat{SKP}(220)=8,12 e^{0,0365\cdot 220}\approx 24,9\cdot 10^3\)
Järelikult mudel annab 2019. aasta USA SKP prognoositavaks väärtuseks 24,9 triljonit dollarit. Tegelik väärtus oli 21,433 triljonit dollarit (The World Bank)
Sageli sobib mudelina kasutada ruutfunktsiooni
\(y=ax^2+bx+c\)
Ka seda saame lineariseerida, kui võtame kasutusele uue tähistuse \(z=x^2\). Saame lineaarse mudeli, kus on kaks tunnust z ja x:
\(y=az+bx+c\)
Mitmese regressioonmudeli hindamine on analoogne hariliku lineaarse mudeli hindamisega. Kasutatakse harilikku vähimruutude meetodit OLS. Lähemalt vaatame seda järgmises teemas.
Niimoodi, kasutades tunnuste teisendamist, saab lineariseerida erinevaid mittelineaarseid mudeleid. Lineariseerimine on vajalik selleks, et mudeli parameetrite hindamiseks saaksime kasutada OLS meetodit.
Toome ära tähtsamad ökonomeetrias kasutatavad mudelid. Esimene mudel on lineaarne, ülejäänud mittelineaarsed, kuid lineariseeritavad. Tabelis on toodud ka valemid piirkalduvuse ja elastsuskordaja arvutamiseks.
| Mudeli nimetus | Mudeli kuju | Piirkalduvus \(\frac{d y}{d x}\) |
Elastsuskordaja \(\frac{x}{y}\frac{d y}{d x}\) |
|---|---|---|---|
| lineaarne mudel | \(y=b+ax+u\) | a | \(a\frac{x}{y}\) |
| log-log mudel | \(\ln y =b+a \ln x +u\) | \(a\frac{y}{x}\) | a |
| log-lin mudel | \(\ln y =b +ax+u\) | ay | ax |
| lin-log mudel | \(y = b + a \ln x +u\) | \(a\frac{1}{x}\) | \(a\frac{1}{y}\) |
| ruutfunktsioon | \(y=ax^2 + bx +c +u\) | \(2ax+b\) | \(\frac{x}{y}(2ax + b)\) |
| hüperboolne mudel | \(y = b + a \frac{1}{x} +u\) | \(-a\frac{1}{x^2}\) | \(-a\frac{1}{xy}\) |
On näha, et palju tuleb tegemist teha logaritmidega, seepärast on kasulik üle korrata logaritmide arvutamise ja teisendamisega seotud põhitõed. Selleks võib kasutada antud teema juures eraldi toodud materjali "Logaritmide kordamiseks".