Previous
Next

3. Harilik vähimruutude meetod.

Olgu meil mingi valim n objektist, millel on kaks tunnust, st meil on arvupaarid (xi, yi), i=1,..., n. Diagrammil  on need arvupaarid kujutatud punktidena.


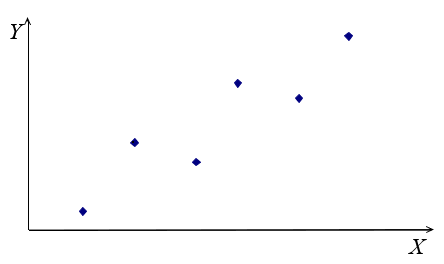
 Lineaarset mudelit kirjeldab graafiliselt sirge \({\hat y_i} = \hat a{x_i} + \hat b\). Siin \( \hat a \) ja \(\hat b\) on mudeli parameetrite a ja b hinnangud, mis meil tuleb leida. \(\hat y_i \) on i-nda punkti koordinaadile xi vastava sirgel oleva punkti y-koordinaat ehk silutud väärtus. Seega tuleb meil leida seda punktiparve läbiva parima sirge võrrand. Aga läbi punktiparve võib tõmmata palju sirgeid. Näitena toodud kolm sirget: roheline, punane ja sinine. 


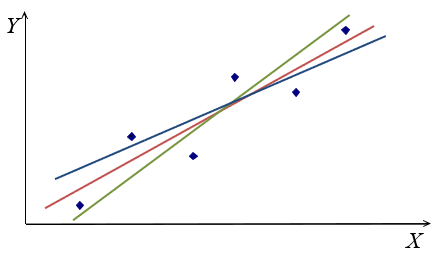
Milline neist kirjeldab seda punktiparve kõige paremini? Vaja on objektiivset arvulist kriteeriumi!

Sellise kriteeriumi leidmiseks leitakse kõigepealt silutud väärtuste \(\hat y_i \) erinevus vaatlusandmetest \(y_i\) mis on hälbed ehk jäägid (residuals):

\({u_i} = {y_i} - {\hat y_i}\)

Järgmisel diagrammil on kujutatud i-nda punkti jääk ühe väljavalitud sirge korral.


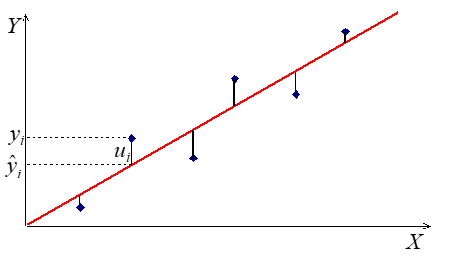
Kui meil on n punkti, saame ka n jääki. Kriteeriumiks on vaja aga üht suurust. Selleks sobib jääkide ruutude summa \(\sum\limits_{i = 1}^n {u_i^2} \).

Vähimruutude meetod: regressioonmudeli parameetrite hinnangud leitakse nii, et jääkide ruutude summa on minimaalne.

\(\sum\limits_{i = 1}^n {u_i^2} \; \to \;\min \)

Nüüd on meil olemas arvuline kriteerium, mille abil saame võrrelda erinevaid sirgeid. Järgmises demos on samuti antud üks punktiparv ning saad proovida erinevaid sirgeid ning nende võrdlemiseks kasutada hälvete ruutude summat. Proovi leida selline sirge, mille korral hälvete ruutude summa on minimaalne.


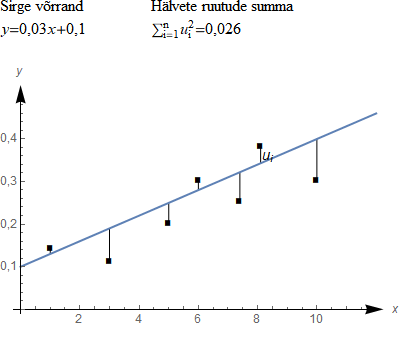
Demos said ka võrrelda enda poolt valitud sirget parima sirgega, mille parameetrid leiti valemite abil. Sirgete võrdlemise antud kriteeriumi järgi võib ju usaldada arvutile. Aga kuna läbi punktiparve võib tõmmata lõpmata palju sirgeid, siis ka ülikiirel arvutil kulub parima sirge leidmiseks lõpmata palju aega. On lihtsam tee: kasutada parameetrite a ja b hinnangute leidmiseks valemeid.

Kuidas nende valemiteni jõutakse? Hälbed võime avaldada tundmatute \(\hat a\) ja \(\hat b\) kaudu:
\({u_i} = {y_i} - {\hat y_i} = y_i-(\hat a x_i +\hat b) = {y_i} - \hat a{x_i} - \hat b\)
Meil tuleb minimeerida hälvete ruutude summat RSS ( Residual Sum of Squares)
\(RSS(\hat a,\hat b) = \sum\limits_{i = 1}^n {u_i^2} \; = {\sum\limits_{i = 1}^n {\left( {{y_i} - \hat a{x_i} - \hat b} \right)} ^2}\; \to \;\min \)
See tähendab, et tuleb leida kahe muutuja funktsiooni \(RSS(\hat a,\hat b)\) miinimumkoht. Matemaatilisest analüüsist on teada, et selleks tuleb I järku osatuletised panna võrduma nulliga
∂RSS(a^,b^)∂a^= 0∂RSS(a^,b^)∂b^= 0\left\{ \begin{array}{l}\frac{{\partial RSS(\hat a,\hat b)}}{{\partial \hat a}} = \;0\\\frac{{\partial RSS(\hat a,\hat b)}}{{\partial \hat b}} = \;0\end{array} \right.

Seejärel tuleb lahendada saadud võrrandsüsteem. Lahendus on toodud näiteks Statistika õpikus (Sauga) lisas A.9. Valemid lineaarse mudeli parameetrite leidmiseks on
a^=∑xiyi-n x¯ y¯∑xi2-n x¯2b^=y¯-a^x¯\left\{ \begin{array}{l}\hat a = \frac{{\sum {{x_i}{y_i} - n\,\bar x\,\bar y} }}{{\sum {x_i^2 - n\,{{\bar x}^2}} }}\\\hat b = \bar y - \hat a\bar x\end{array} \right.

Neid valemeid kasutavad kõik statistika ja ökonomeetria paketid, kus on olemas vähimruutude meetod.

On võimalik näidata (Gauss-Markovi teoreem), et sel moel leitud hinnangud on
  • nihketa;
  • efektiivsed, so vähima dispersiooniga kõigi nihketa lineaarsete hinnangute seas;
  • lineaarsed vaatluste yi suhtes

KUI kehtivad klassikalise lineaarse mudeli eeldused.

Järelikult ei piisa mudeli parameetrite hinnangute leidmisest. On vaja ka kontrollida, kas neid hinnanguid võib usaldada, st kas vajalikud eeldused on täidetud. Vastavaid eeldusi ja nende testimist vaatame järgmises teemas.

Kui CLRM (Classical Linear Regression Model) eeldused on täidetud, annab vähimruutude meetod parima lineaarse nihketa hinnangu BLUE (Best Linear Unbiased Estimator).

Eelnevalt oli meil soov leida Houthakkeri andmeid kasutades mudel, mis kirjeldab elektrienergia tarbimise sõltuvust tarbija sissetulekust Suurbritannia linnades. Mudelit otsime kujul \({y_i} = b + a{x_i} + {u_i}\), kus y on elektrienergia tarbimine (kWh aastas) ja x elanike sissetulek (GBP aastas). Regressioonmudeli hindamise aruande esimene osa programmis Gretl näeb välja selline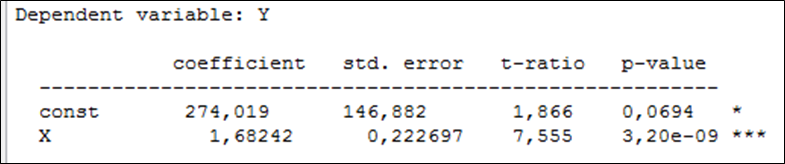



Veerus coefficient on parameetrite hinnangud: konstant ehk vabaliige ja tunnuse x kordaja. Järelikult
parameetri b hinnang \(\hat b \approx 274\);
parameetri a hinnang \(\hat a \approx 1,68\)
ning mudel \({y_i} = 274 + 1,68{x_i} + {u_i}\).

Regressioonmudeli aruande struktuur on ühesugune kõigis statistika- ja ökonomeetriapakettides. Gretli aruande põhjaliku selgitusega võib tutvuda siin. Enamike aruandes toodud suurustega tutvume selle ja järgmiste teemade juures.

Previous
Next