Harilik lineaarne regressioonmudel

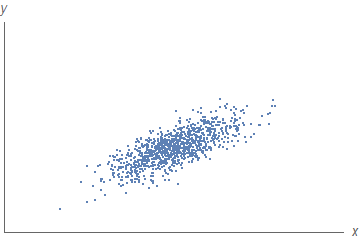
Olgu meil kaks arvulist tunnust x ja y ning n objekti, mille jaoks on nende tunnuste väärtused teada.  Siis saame moodustada n punktipaari (x_i, y_i) ja kanda need punktid  x-y teljestikku. Sellist diagrammi nimetatakse hajumisdiagrammiks (scatter diagram).

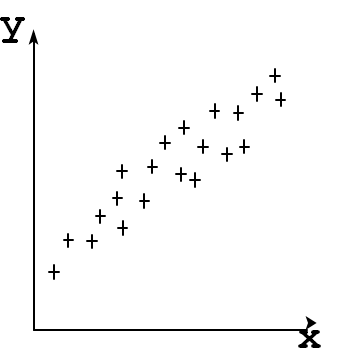
Hajumisdiagrammilt näeme, et kui x suureneb, siis keskmiselt suureneb ka y. Seega nende tunnuste vahel on seos. Ka järgmisel hajumisdiagrammil on tunnuste x ja y vahel seos, kuid punktid on rohkem hajunud.

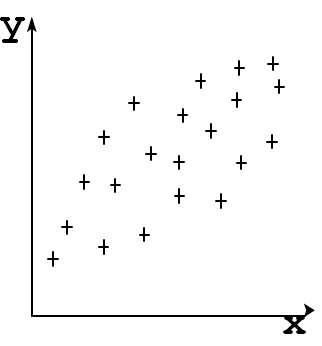
Kuidas väljendada selle seose tugevust kvantitatiivselt?

Ühe suuruse hajumist väljendab dispersioon

 \({\sigma ^2} = E\left[ {{{\left( {X - {\mu _X}} \right)}^2}} \right]\), 

kus E tähistab keskväärtust ja \({\mu _X} = E[X]\) on suuruse X keskväärtus. Diskreetseid väärtusi omava tunnuse korral \({\sigma ^2} = \frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {{x_i} - \bar x} \right)}^2}} \)

Kahe suuruse koosmuutumist väljendab kovariatsioon

\({\sigma _{XY}} = E\left[ {\left( {X - {\mu _X}} \right)\left( {Y - {\mu _Y}} \right)} \right]\)

Termin kovariatsioon tähendab koos muutumist (covariation). Diskreetseid väärtusi omava tunnuse korral 

\({\sigma _{XY}} = \frac{1}{n}\sum\limits_{i = 1}^n {\left( {{x_i} - \bar x} \right)\left( {{y_i} - \bar y} \right)} \).

Erinevalt dispersioonist võib kovariatsioon olla nii positiivne kui ka negatiivne ja jääb vahemikku

\( - {\sigma _X}{\sigma _Y} < {\sigma _{XY}} < {\sigma _X}{\sigma _Y}\)

kus \(\sigma _X\) ja \(\sigma _Y\) on vastavalt tunnuste X ja Y standardhälbed. 

Positiivne kovariatsioon: suurematele X väärtustele vastavad keskmiselt suuremad Y väärtused, väiksematele X väärtustele väiksemad Y väärtused.

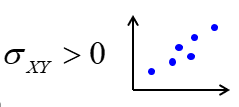
Negatiivne kovariatsioon: suurematele X väärtustele vastavad keskmiselt väiksemad Y väärtused, väiksematele X väärtustele suuremad Y väärtused.

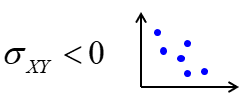
Kovariatsiooni omadused.

1. Sümmeetrilisus \({\sigma _{XY}} = {\sigma _{YX}}\)
2. Kui X=Y, siis \({\sigma _{XX}} = \sigma _X^2\)
• Kovariatsioon on dispersiooni üldistus.
• Dispersioon on kovariatsiooni erijuht:  kovariatsioon iseendaga.
3. Sõltumatute juhuslike suuruste kovariatsioon on võrdne nulliga, \({\sigma _{XY}} = 0\)
   
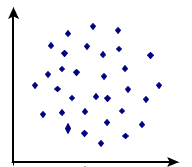
• Rõhutada tuleb, et vastupidine ei kehti, st kui kovariatsioon on null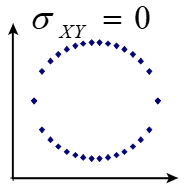, ei pruugi suurused olla sõltumatud. Näiteks  joonisel on tunnuste vahel tugev mittelineaarne seos, kuid kovariatsioon sellise punktiparve korral on 0. 
4. Kui σ_XY ≠ 0, siis nimetatakse suurusi X ja Y korreleeruvateks.

Kovariatsiooni puudus on, et see on ühikuga suurus ja seetõttu pole võimalik võrrelda erinevates ühikutes antud tunnustepaaride kovariatsiooni. Valemist tulenevalt on kovariatsiooni ühikuks tunnuse X ühik korda tunnuse Y ühik. Näiteks tahame võrrelda, kumb suurus on Eesti maakondades tugevamini seotud töötuse määraga (%), kas keskmine kuupalk (€) või sündinud ettevõtete arv aastas. Leides vastavad kovariatsioonid, saame:

kovariatsioon töötuse määra ja keskmise kuupalga vahel -84,9 % ·€

kovariatsioon töötuse määra ja sündinud ettevõtete arvu vahel -480 % ·ettevõtet

Näeme, et mõlemad sosed on negatiivsed, st mõlema tunnuse tõustes töötuse määr väheneb, aga kummaga on töötuse määr tugevamini seotud? Leitud arve ei saa võrrelda, sest need on erinevates ühikutes. Ja me ei saa ka hinnata seda, kas seos on tugev või nõrk, sest me ei tea, milline kovariatsiooni väärtus vastab perfektsele seosele. Selle võib küll eraldi välja arvutada, see on standardhälvete korrutis.

Seepärast normeeritakse kovariatsiooni nii, et saaksime ühikuta suuruse ja selle absoluutväärtuse maksimaalne väärtus oleks 1. Võrratusest  \( - {\sigma _X}{\sigma _Y} < {\sigma _{XY}} < {\sigma _X}{\sigma _Y}\) näeme, et selleks tuleb kovariatsioon läbi jagada standardhälvete korrutisega. Niimoodi leitud suurus on korrelatsioonikordaja 

\({r_{XY}} = \frac{{{\sigma _{XY}}}}{{{\sigma _X}{\sigma _Y}}}=\frac{\sum(x_i - \bar x)(y_i - \bar y)}{n \sigma _x \sigma _y}\)

Korrelatsioonikordaja on ühikuta suurus ning selle väärtus on -1 ja 1 vahel:

\( - 1 < {r_{XY}} < 1\)

• Korrelatsioonikordaja absoluutväärtus näitab seose tugevust.
• Korrelatsioonikordaja märk näitab seose suunda: positiivne või negatiivne.

Näiteks olgu meil tunnused A, B ja C. Soovime teada saada, kumma tunnusega on A tugevamini seotud, kas tunnusega B või tunnusega C. Leiame vastavad korrelatsioonikordajad:

r_AB= 0,58 ja r_AC = -0,87.

Nagu näha, on A ja C vahel tugevam seos kui A ja B vahel, sest korrelatsioonikordaja absoluutväärtus on suurem.

Testi ennast, kas oskad korrelatsioonikordajate põhjal teha õigeid järeldusi.

Rõhutada tuleb veel seda, et korrelatsioonikordaja näitab lineaarse seose tugevust, kui hästi on punktid koondunud ümber sirge. Seepärast nimetatakse seda ka lineaarseks korrelatsioonikordajaks. Mittelineaarse seose tugevuse hindamiseks see näitaja ei sobi. Siis kasutatakse näiteks Spearmani astakkorrelatsiooni.

Järgmises demos saad uurida, kuidas on omavahel seotud lineaarne korrelatsioonikordaja ja punktiparv hajumisdiagrammil.

Edasi vaatame üht reaalsetel andmetel põhinevat näidet. H.S. Houthakker analüüsis oma artiklis "Some Calculations on Electricity Consumption in Great Britain." , millega on seotud elektrienergia tarbimine Suurbritannia erinevates linnades. Andmed pärinesid 42 linnast aastatest 1937-38. Tarbija sissetuleku ja elektrienergia tarbimise vahel oli positiivne korrelatsioon, r=0,767. Hinna ja tarbimise vahel oli nõrk negatiivne korrelatsioon, r = -0,274.

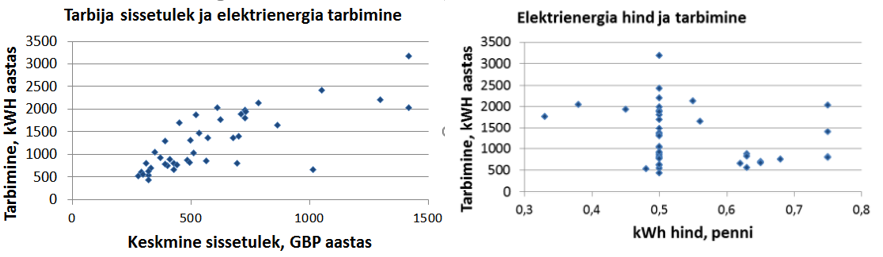
Nagu näha, on tarbija sissetuleku ja elektrienergia tarbimise vahel päris tugev seos. Edasi tekib küsimus: kas on võimalik leida seda seost kirjeldavat matemaatilist mudelit? Et teades tarbija sissetulekut, saaks prognoosida elektrienergia keskmist tarbimist. On küll võimalik ja selleks tuleb hinnata vastavat regressioonmudelit.